


figure out format of submission! cb 4 may 2011
This is a grab-bag of projects: Please do at least two.
Your goal is primarily the written report of your work. The expectation is that you'll be using various sources for your investigations, so make sure you cite all references you used: the more (that you actually use) the better. Technique, results, and presentation (especially graphics) are all important. The elegance and organization (and correctness) of the code count, but not as much as the report, which should contain enough information to convince the reader that your code must be correct.
The SIDC has lots of sunspot activity data, I got some and put it in the Data folder for you to download. ssdata.mat is a file of monthly sunspot activity data going back to 1759, with the associated guide ssdatareadme.txt. Go read up on sunspot activity cycles, report on what you find, and see if you can verify or falsify claims from the literature by analyzing this data. If you want to look at daily or yearly data, SDIC has that too.
You've seem the Lorenz attractor in Intro. DE Paper . Read more about Lorenz Attractors and Strange Attractors in the usual places (Wikipedia, Google). Try Strange Attractors.
Use your Lorenz attractor implementation from the ODE topic, or go ahead and implement it (it's a 4-line program with a 4-line ubroutine). The output is four arrays, T, X, Y, Z, where we think of a point following a path in 3-space: at time t it is at X(t), Y(t), Z(t). Plotting two of these against each other (as in plot(X,Z) ) gives the familiar "Lorenz Butterfly Diagrams".
Instead, consider the function, X(t), Y(t), Z(t). They must exhibit some periodicity to give those spirals we see in the diagram. As usual, see what you can find in the literature, if anything, on the subject. Then produce some data and analyze its frequency content. Things you can vary are: the axis (X,Y,Z) you plot and the parameters of the Lorenz DE.
Matlab has commands sound and soundsc, but I only used wavplay, wavrecord, wavread, and wavwrite. See getsound.m, putsound.m in code directory. The arrays wind up as doubles I think, but certainly as floating point numbers, and nicely enough any array of floats varying between -1 and 1 can be wavwritten as a wav file: so we can create our own sounds like pure sine, square, sawtooth waves easily.
For no good reason I used stereo wav arrays (2-columns) for time-domain work (Project 4) and mono for the frequency domain (Project 5) and the Spectrogram (Project 3).
wavread has many options, including getting meta-information (sampling rate etc) and reading big files in manageable sequential chunks. Our Data File has at least one ".wav" file in it, but there are heaps of them of all sorts out on the web, or you can make your own with a microphone, CD player, iPod, whatver.
The Simpson's theme in the data directory, and indeed most if not all of the ".wav" files on the web are actually .mp3 files, which wavread can't read (you'll get an error message). What you do is download the (bogus, MP3) ".wav" file, and if you're on one of the UR machines (I don't know what's standard on random Windows systems) go All Programs - Multimedia - Real - RealPlayer Converter. (Audacity won't read these mp3s it seems). Otherwise there are many converters out there: on Mac's OS-X system, Switch works. Convert the .mp3 to a real .wav file (thus uncompressing it) and Matlab should be happy with the result. Usually converting means no more than loading the file and exporting or saving as a .wav file. You should be asked for the .wav encoding parameters, especially samples per second.
Warning! CD quality is about 44 KHz. (standard Matlab setting is 44100 samples/second). The 11025 setting is listenable and standard. For my work I used 22050. Those three are considered standards. Even at the 11025 setting, the .wav file will be about ten (10) times as large as the .mp3 file (gives you respect for mp3, eh? You might look up what all went into this clever encoding). So you probably don't want to deal with more than a few seconds of .wav sound at a time.



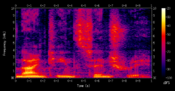
Above left (from Wikipedia) is a spectrogram of Male voice saying "19th century": vertical strips are pseudo-colored power spectra (color guide at right of image), time goes left to right. Middle and right is CB's version, showing the spectrogram of two constant-frequency sine waves and one that increases in frequency with additive uniform zero-mean noise. Here, frequency reads down, time goes left to right. There are 10 vertical strips. Matlab shading is interp in the middle and faceted (default) on right.
Read Wikipedia on 'sonogram' and 'short term fourier transform'. Write a spectrogram program you can use to display speech or music waveforms Just Like Downtown (as above).
If you're interested in language, maybe read about 'formants', collect a few samples of speech and see if you can identify the formants in your sonograms. If not, maybe analyze some of your favorite music and describe what the sonogram is showing us.
I wanted to know something about guitar effects. For these two
projects
I'm giving you my code ,
which probably has more never-do-this
howlers than it has good ideas.
You are invited to use it, improve it,
or extend it as your interests take you. Just put in some work and
tell us what you did in your report, which will be an HTML page with
pointers to your sound samples. I think you can improve everything I
did or you can add something new...wah-wah pedal, ring modulator, phase-
shifter, effects I never heard of, whatever. I only used first-level
Google and Wikipedia for how-to's. If you want to apply my code or
modify it, the exercise is in understanding and using someone else's
ratty code. Main thing is you have fun, process signals, and learn
something.
Go to
Guitar Effects Explained
.
In fact, if this flakey site is misbehaving, just look up
"chorus effect", "phaser effect", "flanger" "ring modulator", etc.
on Wikipedia. Our goal is to understand how to implement these
effects digitally, not necessarily to understand all the math
(if any) or diagrams. I think it will be clear how to
take some sound waveform data and implement
our choices from
chorus ,
phase-shifter ,
flanger ,
delay ,
ring-modulator .
All this work can be done in the time-domain just by shifting,
multiplying, and adding time-signals. In this business they seem to
call a small shift a "phase shift" and a big one a "delay".
Fair enough, they're at different timescales.
Acknowledging my ignorance about how proprietary products work, and realizing
we're stuck in a digital, not continuous, world, the section below
gives my understanding.
Code I wrote (no guarantees on content OR style!) are in the
SP code directory.
PRACTICAL TIP. One of my basic coding principles
is When Developing Code, Always Be Able To Tell If An Output
Is Reasonable Or Gibberish. So there's a
Corollary: Never Use Real Data Until Last Minute.
These principles account for the possibly puzzling plot
commands in my sound code. That's because I started off
not using getsound at all -- I started off generating my
own simple-minded inputs, like a single sine wave or ramp (straight
line function), to see how it was affected by my effects. A delay
should cause a visible shift. A swept delay should cause the output
sine wave to lead and then follow the input. Etc.
See getsound.m, putsound.m in code
directory. The arrays wind up as doubles I think, but certainly as
floating point numbers, and nicely enough any array of floats varying
between -1 and 1 can be wavwritten as a wav file: so we can create our
own sounds like pure sine, square, sawtooth waves easily. For no good
reason
I used stereo wav arrays (2-columns) for time-domain work and mono for
the frequency domain (below).
Given a wav array (Sound, say), it's easy to delay it: assume
it's preceded by zeroes and so delayedSound(i) = Sound(i-Delay);.
Issues arise because we usually like to think about
delays in seconds (echoes) or milliseconds
(for flangers, say), or somewhere in between for other effects.
So we need to convert from Hz to indexes, and
that depends on the sampling frequency.
This motivates my various unit-changing utilities.
Can we simulate someone singing or playing sharp or flat with time-domain
techniques?
Not simply! We can take every other sample in a wav array
and get one which, played back at the same rate, is an octave higher.
BUT it's only half as long.
If you want achieve the
Alvin Effect ,
you've got to sing at half speed and THEN speed up your playback or
sample down.
Likewise interpolating samples twice as frequent as the original
wav array gives you an octave down and twice as long.
You should understand linear interpolation, since it's basic.
The code's in the directory, but the idea is just that if you have
two points (x0,y0) and (x1,y1), if you approximate the function between
them by a straight line, the value of an x that is p percent of
the way from x0 to x1 is the "interpolated" value of y that is p
percent of the way from y0 to y1.
For a chorus effect I need the voices to pretty much stay together.
I do have a "constant delay" effect, which just shifts the wave in
time (array index).
For my swept "Delay"
effects (see the reading for concepts like Sweeping, Sweep Depth,
etc.), I (sinusoidally) sweep, or increase and decrease, the resampling
rate to create a distorted version.
The new 'voice' alternates between being lower and slower
and being higher and faster,
so on the average it doesn't fall behind the original.
Thus we have a function f given by the sweep waveform and
parameters that tells us in this case how 'delayed' (or 'advanced')
the sample at Wnew(i) should be: what sample from Worig gets written into
Wnew(i)? Usually the 'sample index' from Worig is not an integer, hence
our need to interpolate Worig to get values for Wnew.
So we just work through Wnew's
indices i = 1:N, computing (from a function f given by sweep waveform and
parameters) a 'delayed' (could be negative) x value f(i). Interpolate
f(i) into the original wav array and the result is the value at
to re-sample at some x+dx.
My delay effect has several parameters: I use an exponentiated sine as
a sweep function: Raising the sine to fractional powers makes for a
faster rise and fall, approximating a square wave as the exponent
shrinks. Positive exponents make the wave stick near 0 more, and have
sharper peaks. In my experience fast changes in sweep lead to annoying
discontinuities, but more experimentation is needed.
As parameters, I have the amplitude (sweep depth), frequency, and
phase of the sweep wave,
maximum and minimum delay in
milliseconds, and a final volume for the voice.
My pitch effect really does exactly the same thing but with different
semantics (and implementation -- probably not necessary). Instead
of microseconds the sweep is over sharp to flat pitch variations in
terms of half-steps (a sampling rate of 21/12 = 1.0595 will raise
the pitch one half step). The pitch of a sound varies with the rate of
sampling, and so the effect simulates a sampler that runs faster and
slower, again averaging out to zero delay.
With a single sine wave, say Concert Pitch A440, the pitch effect
would not so obviously display the tempo changes (but the highest
pitches still last longer than the lowest). Here's
A440 , and here's the output of my
pitch effect ,
which goes sharp and flat at the rate of 1 Hz.
Now if these were evenly-sampled
waves you'd expect to get some cool microtonal exercise increasing and
decreasing dissonance by adding these two waves up.
Instead, since they also speed up and slow down, you get a
mess.
My final time-domain effect is simply 'vibrato', which for me is
sinusoidally varying the amplitude of the elements in wav array,
so the same sound gets periodically louder and softer.
Compare this Solo and
the baritone quintet
version. There's one pure delay (25ms), one swept delay (30-50 ms),
one swept pitch variation ( ± a semitone), one vibrato (20% at 10hz)
and a cascaded pitch variation + vibrato voice.
All those voices sort of blur together and average out... could be more
dramatic as a carefully selected trio.
Now flanging turns out to be exactly the same thing as swept delay
except the delay is around 1-10 ms, and often flangers have several
stages (operate on the input sequentially, with stages feeding into
one another or back to themselves).
Here is my version of a
rhythm section , a
flanged version with a sweep
depth from .1 to .4 ms, then that
fed back (in series) 3 times , and
2 flangers in series (The
previous and one with sweep from 2 to 10 ms.
To do the chorus effect, you need to vary pitch a little.
How would you raise all the pitches in a sound file up a half-step?
If all the frequencies were multiplied by two (the frequency component
for 200 Hz in the input is moved to 400 Hz in the output, etc.),
the whole voice or orchestration or generally sound would go up an octave
(12 half-tones). So to shift up a half-step we need to multiply
all the frequencies by the twelth root of 2, or 2 1/12.
Now there's a problem. Imagine the power spectrum PS of our original
sound wave, displayed in "fftshift" form, symmetrical around the
center: Imagine it's indexed from -N:N.
If we move the power values to a new array HighPS where
they have twice the frequency,
then PS(1) goes to HighPS(2), 2 goes to 4, N/2 goes to N, and N/2 through
N go nowhere! We've lost 1/2 the values defining what the original
wave was. There may be less energy up there but high frequencies are
definitely important
for sounds like ssssibilants and ffffricatives, anyway. oops.
Below, I broke the wav array (created by sampling
at 22050 samples/sec) into 8192 -long
segments (this is the time domain, remember)... so that would be
8192/22050 = .3715 second-long segments, pitch-shifted each, and
pasted
the results together again. (It's the same code that created the sonogram
above, by the way), only computing and displaying the power specta
after the temporal break-up).
Here is a Solo ,
a frequency-domain synthesized
fifth above ,
and a duet , with the
melody and major third above.
There are professional items like real-time
guitar effects, pitch correction apps for iPhone, and voice
transformatioqn. I couldn't find much about pitch correction products
on line, but check this out to see how careful you need to be to work
with human voices:
Voice Transform Site , and take a look at the papers pointed to
early on by Kain & Macon and Yegnaranayana et al.
Impress us with some image reconstruction.
Our Data File
has three .jpg images of license plates but they may be getting
a bit stale. Grab an image from the web, blur it with some 2-D
PSFs and try to recover the original. Good candidates are the
disk (out-of-focus blur), gaussian (very nice numerical properties),
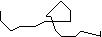
and a 2-D path like the following, presumably represented by an array
of 0's and 1's.
For all these cases, you know the PSF exactly and
mathematically everything should work wonderfully. Does it, and if
not why not?
Try to do reconstruction on an image you make. You could set
up some small light source and make a motion-blurred image: the image
of the small source shoud be your PSF. Then
go in and extract the PSF and do the deconvolution.
Or shoot a picture of a scene through a chainlink fence, venetian blind,
window screen. Then shoot the same picture with a white (say)
background
set up behind the fence, blind, or screen. Now you are in a position
to make a filter that should remove the f,b,or s effect from your
photo of the scene. Does it work, and if not what happens?
See the
Universal Hand-In Guide.
Briefly, for the Code component of this assignment, you'll need a .zip (not .rar) archive with
code files and README.
Submit the writeup as a single, non-zipped .PDF file.
Submit before the drop-dead date for any credit and
before the due date for partial-to-full (or extra!) credit.
Check immediately to see BB got what you sent!
Submit this file to the Signal Processing Assignment in Assignments in Course
Content in Blackboard before the drop-dead date for any credit and
before the due date for partial-to-full (or extra!) credit.
Guitar Effects
Guitar Effects: Time Domain
Project 5: Pitch Adjustment
Project 6: Image Reconstruction
What to Hand In
Last Change: 4/20/2011: RN