
Programming Concepts: Loops (Attaway Ch. 4)
Quibble Question
Why is the Firth of Forth Famous?
Looping: CS Theory
Computer Science Theory tells us:
-
If programs had a fixed sequence of execution,
or even included repetition any pre-computed number of times,
computers would be less powerful than they are (i.e. could compute
answers to fewer questions no matter how long they computed).
-
With I/O, bit-manipulation operations (e.g. arithmetic), AND
any type of looping or iteration construction
that allows repetition subject to
a condition computed in the loop,
All computers become equally powerful i.e.,
they can compute any 'computable' function (given time). (!!)
This is known as the
Church-Turing Thesis.
-
Non-computable function? e.g. a program P to determine if any other
program halts (as opposed to going into infinite loop). Why? easy:
use P to write a program that reads itself and then halts
if it doesn't halt and loops if it does halt. Contradiction, so
P cannot exist.
-
There are infinitely more non-computable real numbers than computable
ones. In fact there are only as many computable reals as there are
integers. Why? easy: you can describe any program with a single
(large) integer: e.g. just concatenate the ASCII codes of its characters.
Looping: Practical
Repetitive operations "R" computers. E.g.:
- Do the same thing to every one of a large number of items.
- Produce tables.
- Perform some computation over and over until "done" like
adding the next term to an infinite series, running a simulation
- Operating systems: more or less
glorified "read, evaluate, print" loops.
Counted loops
(
primitive recursion in recursive function theory):
perform loop some given number of times
(e.g., "brush hair 100 strokes before bed.").
Conditional loops
(
general recursion):
repeat until done
(e.g., "whip until fluffy")
Vectorized Commands as Hidden Loops
In Matlab, since matrices are the
primary datatype, explicit looping is often not needed.
Vectorized commands operate on entire matrices.
With Matlab we take this for granted, but it's both a luxury and a
curse: a powerful capability that can be misused.
Attaway often refers to vectorized versions of commands as
"efficient". They are terse to us humans, but in fact
vectorized commands are implemented under the hood as loops,
so they can't be inherently more efficient in terms of execution time.
For example,
avec = sqrt(bvec*5 + 4);
is_greater_vec = some_vec > 5.0;
% produces logical vector
Good Rule: create a matrix or vector if you really need all its values
(say to make a plot or as input for further processing). Do
not construct a vector to hold input that can be generated
and used one piece at a time.
For instance, to add all the numbers
from one to a billion, we don't need a billion-long vector[1,2,3...].
We need one variable to hold the sum and we
need to count: to generate the numbers
to be summed one at a time. We need a for loop.
The vectorized
sum(1: 1000000000) (sum one to a billion)
gives an out-of-space error, but
total = 0;
for value = 1:1000000000
total = total + value;
end
after running for several seconds, actually produces an
(approximately) correct result.
For Loops (Attaway 4.2)
Sometimes called a "do loop" (for Fortran), a for loop
implements counted loops.
Reserved words: for, end,
(continue,
break, return).
for loopvar = range_expr
statements;
end
Executes the statements (down to the for's matching
end statement) once for every assignment to
loopvar from elements of range-expr.
-
A for loop always creates an index variable
(sometimes called a loop variable) that
is usually used in the loop, but may not be. Above it is called
loopvar.
- The
range-expr must be a range: one of the
simplest looks like 1:N, and the most trivial looks like
3. The trivial case only "does the loop once", so we don't
need
the loop!
- Forms like for n < 5 ... are syntactically invalid.
- If x is a number, a form like
for loopvar = x*2 + 10
statement;
statement;
end
executes the statements once with the value of the expression.
- Vectors are valid ranges, which provides an useful way of looping
with an arbitrary set of index values.
The range expression can be pretty general: Possibilities include operator
expressions and vectors.
for loopvar = 1:N
for loopvar = 10:2:20
for loopvar = x: 2*y: z+150
for loopvar = [2 5 -98 13 pi]
% sets loopvar to each element
for loopvar = some_vec
% sets loopvar to each element
Index Variables
The index variable is so-called because it is so often
used as an array index, in essence to find the
address of the value we want.
-
In many programming languages variable names
i and j
are generically used for index variables(xi, get it?).
-
In Matlab, this can lead to problems, since
i and j are
pre-defined constants that represent sqrt(-1). If you
assign to these variables, you will lose Matlab's intended semantics for them.
Two Simple Examples
Enthusiastic hello:
for repetitions = 1:3 % i is set from 1 to 3
% but not used in loop!
disp('Howdy!');
end
Accumulator problem: accumulate partial answers into a single
answer variable (very common).
For example, compute sum of n2, as n goes from 1 to 10.
sumsq = 0; % a box for sum, initialized to 0
for n = 1:10
sumsq = sumsq + n^2; % update and save sum
end
Some Bad Examples
What happens if we try the following?
for n = 1:10
sumsq = 0; % a box for sum, initialized to 0
sumsq = sumsq + n^2; % update and save sum
end
Above runs fine, just probably not what we want. So that's
a problem... no error message.
On the other hand if we make up our own syntax and come out with gibberish like:
y = for x < 5
sum +x
end
We see an unhelpful
Illegal use of reserved keyword "for".
Which is technically right but
pretty vague. And since there are other problems in our little loop
above, either fixing one problem (or making it worse!)
is only going to lead to another useless error message. You're dying
here.
Moral:
Trying to rewrite code without understanding what has gone wrong
(aka Programming at Random) usually doesn't work.
- STOP, THINK, READ THE BOOK, TYPE HELP.
- Make sure you understand what the problem is you are trying
to solve, and how to solve it. If you don't, there is no way you can tell
a computer how to do it. Computers have no sense, common or otherwise.
- Try printing out values while inside the loop.
- Try pausing at the end of each iteration, and making sure
that all your variables have the value you think they ought to.
- Try a simple case for which you know the answer and watch where
the program goes astray when it tries to compute it.
- If all else fails, pause the program after each step and make sure
it is doing what you want it to.
More Bad Examples
More horrible examples of how NOT to
Compute sum of n2, as n goes from 1 to 10.
Try to figure out what each of them will do...
sumsq = 0; % a box for the sum, initially 0
for n = 1:10
% n^2; % no
% sumsq = n^2; % no
% sumsq(n^2); % no! Stop Guessing!!!
end
Examples using accumulators:
Assume the following script is stored in for_script.m.
vecsum = 0; % a sum accumulator
vecprod = 1; % a product accum. (why not 0?)
N = length(a_vector);
for indexvar = 1:N % indexvar goes from 1 to N
vecsum = vecsum + a_vector(indexvar);
% add into accum.
vecprod = vecprod * a_vector(indexvar);
% mpy into accum.
end
vecsum
vecprod
Then
>> a_vector = 1:2:9; % = [ 1 3 5 7 9]
>> for_script
vecsum = 25
vecprod = 945
Several ways NOT to get the sum...
vecsum = 0;
N = length(a_vector);
for indexvar = 1:N % indexvar goes from 1 to N
% vecsum = sum; % syntax error
% vecsum = sum(1:N); % computes wrong sum N times
% indexvar; % what???!!!
% vecsum + indexvar; % computed and discarded.
% vecsum = vecsum + indexvar; % wrong sum
end
True, Matlab has built-ins for vector sum and product, but
we're learning for-loops not memorizing a million Matlab commands.
Study the following examples and use them
for templates. Look up the syntax (Matlab help etc.)
of any construct you are not absolutely sure of.
Computers are very picky about syntax, and will fail
(likely with useless error messages or none at all)
if you stray from the path.
Search Example
A common operation is to step through a number of cases and
remember the "best" or "worse" or "smallest", etc.
A standard approach is to create a "minimum" variable,
assign the first element in a list (vector, matrix...) to it, and
loop through the rest of the elements replacing the minimum if you
find a smaller element (Att 4.1.2).
function [min_val, min_index] = myminvec(vec)
min_val = vec(1);
min_index = 1; % Don't forget this!!
for index = 2:length(vec)
if vec(index) < min_val
min_val = vec(index);
min_index = index;
end % if
end % for
end % function
Again, matlab has
min,max built-ins, and even a variant that
returns the minimum and its index, as above! But we're learning
programming here, not memorizing idiosyncratic matlab-only features.
Notice matlab's min can take a matrix but then has
a possibly surprising result.
>> y = [ 4 -1
2 7];
>> min(y)
ans = [2 -1] % mins of columns (!)
>> min(min(y))
ans = -1
More Examples: Mundane and Bizarre
Add all positive elements of a vector vec
PosSum = 0;
for ndx = 1:length(vec)
if vec(ndx) > 0
PosSum = PosSum+vec(ndx);
end
end
Reverse a vector.
avec = [ 1 1 2 3 5 8 13];
N = length(avec);
backvec = zeros(1,N);
for forward_ndx = 1:N
backwards_ndx = N-forward_ndx+1;
backvec(backward_ndx) = avec(forward_ndx);
end
backvec
backvec =
13 8 5 3 2 1 1
The following example illustrates
the perils of data-type conversion! What's supposed to happen here?
What does happen here?? Very strange... (hint: Attaway 1.5.3.1:
linear indexing)
for ndx_var = [1 2; 3 4]
ndx_var % just report its value
end
ndx_var =
1
3
ndx-var =
2
4
Nested FOR Loops (Attaway 4.2)
It is very common to nest for loops inside of
for loops e.g., to add all matrix elements
function sum = mat_add(A)
% Sum elements of A
% sum is name of MatLab builtin but no conflict (scoping!)
[NRows NCols] = size(A);
sum = 0; % initialize
for row = 1:NRows
for col = 1:NCols
sum = sum + A(row, col);
end % NCols
end % NRows
end % mat_add
This is same as the vectorized
sum(sum(A));
Note that nesting loops results in a dramatic increase in the number
of operations carried out - the product of the the number of elements
in the ranges. This gets out of hand very fast, so loops are
seldom nested terribly deeply.
Please Don't Do This!
Please Don't Do This!!
Exercise 3.30:
function out = choose(in)
in = input('give me a number');
choice = menu('choose a function', 'ceil','round','sign');
.....
Functions talk to other functions! They don't need humans!
Comparative Syntax and Semantics
Diversity!
In Matlab:
for Mndxvar = 1:10
fprintf('\n Mndxvar = %d', Mndxvar);
Mndxvar = 2*Mndxvar;
end
yields
Mndxvar = 1
Mndxvar = 2
Mndxvar = 3
...
Mndxvar = 9
Mndxvar = 10
In C:
#include
main()
{ int Cndxvar;
for (Cndxvar = 1; Cndxvar <= 10; Cndxvar= Cndxvar+1)
{ printf("\n Cndxvar = %d", Cndxvar);
Cndxvar = Cndxvar*2;
}}
yields
Cndxvar = 1
Cndxvar = 3
Cndxvar = 7
Why should we not be surprised?
Return Statement
The return, break and continue
commands are special sorts of goto commands, and so can
lead to confusing and un-structured code.
They should be used judiciously, and mainly in specific situations.
The return statement is the most frequently used of the three.
When encountered in any function or script, it causes a return of control
to the location in the calling program immediately following the
call.
Functions normally return when the code reaches the end of the function.
The return statement simply causes an "early" return.
Since every return statement in a function goes to the same, well-defined
location, there is little opportunity for confusion, and thus limited
opportunity for abuse. Use when convenient.
Break Statement
The break command breaks out of a
for- (or while-loop)
to the statement just after its end.
Consider the following script.
% script forit.m
for i = 1:5
disp(i*i);
end
i
fprintf('\n with break\n');
for i = 1:100
if (i*i) > 75
break
end
disp(i*i);
end
i % end of script
Running the script produces the following:
>> forit
1
4
9
16
25
i =
5
with break
1
4
9
16
25
36
49
64
i =
9
The break statement can be hard for a reader to follow, as
he or she needs to scan ahead to find the end of the current loop
to discover where control transfers.
It is best reserved for situations such as exiting under error conditions,
where other means of getting out would be awkward.
In the preceding example, the break destroys the implicit semantics of
the for loop, as it does not execute the expected number of times.
A better approach would be to use a while loop (next topic)
and make the condition part of the loop proper.
Continue Statement
The continue statement is less
common than break.
it aborts the current iteration of the loop and resumes iterating with
the next iteration of the loop.
Here we want to print out the indices of the positive values in a vector
vec = 2*rand(1,10) -1 % random numbers between -1 and 1
for i = 1:length(vec)
if vec(i)<0
continue
end
i % print if get here
end
Running the above produces:
vec =
Columns 1 through 6
0.52711 0.68345 0.48181 -0.47806
0.92415 -0.28688
Columns 7 through 10
-0.35907 0.62747 -0.64415 0.88629
i =
1
i =
2
i =
3
i =
5
i =
8
i =
10
Note that the code is a bit obscure and hard to follow, and this particular
program would be better written using an if statement.
This is often true, and if you find yourself wanting to use a
continue or a break statement,
you should ask yourself if there is a clearer way of structuring the code.
The most common "legitimate" use of these statements involves cleanly
getting out of nested code when error conditions occur.
WHILE Loops (Attaway 4.4)
For-loops normally repeat a certain, pre-computed
number of times.
In contrast, while-loops continue repeating until a
specified (boolean, true-false) conditional test is met.
Associated reserved words: while, end,
(break, continue,
return).
Since while loops repeat until a certain condition is met,
it is easy to write for-loops using while-loops
but not vice-versa.
Thus in the absence of 'tricks'
(such as using conditional break statements),
while-loops implementing 'general
recursion' are more powerful than for-loops ('primitive
recursion').
The general form of a while-loop is shown below:
while condition-expression
action
end
The condition must be true to get loop started and must become false
sometime or you get infinite loop
(exit one of these with CTRL-C if it happens to you in Matlab).
While loops are good for stopping when you find what you want
(say a negative
value in a vector, or you've reduced an error below some threshold).
FOR or WHILE?
For loops can be implemented with while loops,
but in practice, the choice conveys significant information about how
the algorithm works and it is
important to know when one or other is called for.
Specifically, the choice is:
Do N Times (where we know N in advance)
vs.
Do until job's done (and it's hard to say how long that will take)
Example: for vector X,
for i = 1:length(X)
X(i) = X(i) / 7;
end
divides every element of X by 7. Since we can easily know X's size,
a for loop is appropriate.
On the other hand, suppose we want to add up 1/N for N =
1,2,3... etc. until the sum is only changing very slowly.
Stating this in terms of a change threshold we want to get below is
more natural than trying to figure out the appropriate N beforehand.
Hence a while is appropriate.
denominator = 1;
term = 1/denominator;
sum = 0;
while term > .0001 % we're not done!
sum = sum + term;
denominator = denominator + 1;
term = 1/denominator;
end
sum
sum = 9.7875
(Aside: 1/1, 1/2, 1/3,... is the harmonic series from its
place in the theory of music overtones (unison, octave, fifth,
third...).
What is its infinite sum?)
Other comments:
-
Some languages have a repeat (statements) until (condition)
loop, which always
goes thru the statements once and then checks the condition.
-
The condition can be logical expression (ANDs and ORs...), arbitrarily
complicated.
-
Other uses: counting, (set a sum variable to 0 and increment it in
the while loop) and checking user input for errors (Att 4.4.4-4.4.5).
Break, Continue, Return
Work in while loops the same as in for loops
Break
terminates execution of the loop. In a
nested loop, it leaves the innermost loop (the one it is in).
Continue
stops execution where it occurs and starts execution at the
NEXT iteration of the loop. In a
nested loop, it continues the loop it occurs in.
Return
stops execution of a function and returns immediately
to the calling program.
Straight Talk on Vectorized Commands

Red Ice Creations (www.redicecreations.com)
For this chapter and for the Pi project, please forget about
"vectorizing" your code.
Don't do it!
Refer to matrix elements (Mat(i,j)), not matrices (Mat).
And don't use the : range operator to refer
to rows or columns of a matrix. Use loops.
Don't create matrices for simple series like
'all odd numbers between 3 and 97' that can easily be done by repetition.
On the other hand, for irregularly-spaced data like
[ 1 2 5 10 20 50 100 200 1000],
clearly a data vector is called for.
Mean and Standard Deviation (Attaway 12.1)
We'll be seeing a lot of these, e.g. in Prog. Asst. 3.
Informally, statistics are numbers used to describe collections
of other numbers, or data. Three common ones are the mean
(average), the median,
and the variance ( = standard_deviation2).
We know about means and medians. Do we?.
Variance and standard deviation measures how "spread out" the data are,
how much the various data points differ from their mean value.
If they're all the same, the
variance is zero.
-
Mean of a matrix. Classic accumulator problem.
initialize sum to zero,
Use nested for-loops iterating over rows and
columns, adding M(row, col) to sum.
After for-loops, divide sum by rows*cols.
-
Attaway's not very
helpful on the standard deviation. Her definition is OK in line
3 of 12.1.2 but there's nothing about how to calculate it efficiently,
or why N-1 is used (instead of N) in the denominator.
-
In the limit of large numbers of data points, variance is basically the "second
moment" of the data in a physics context, defined as
Var(X) = E[(X - μ)2], where E is the
expectation
(or Average, or Mean) operator, and μ is the mean of X.
-
If all the X's are close to the mean μ = E(X) the variance is small.
The differences are squared, so they're always positive, and big
differences (referred to as "outliers") contribute a relatively large amount.
The standard deviation σ (X) = √ Var(X).
Computing the Variance
Naive implementation: read and use whole data set twice:
one 1:N for-loop
to calculate the mean, then another 1:N to do the subtraction, squaring, and
addition to find the variance.
But! Notice, in the second moment equation above,
Var(X) = E[(X - μ)2]
= E[X2 - 2 μ X + μ2]
= E[X2] - 2 μ E[X] + μ2
= E[X2] - μ2
= E[X2] - E[X]2
Thus we can calculate mean and variance with only one pass through the data
(one loop).
In the loop that currently calculates the mean by summing
X(i,j),
we just need to accumulate another sum, this one sums the
squares of the elements, X(i,j)*X(i,j). When done
summing (after the for-loops), calculate the mean of the
summed X's and X2's, do
the subtraction and a square root, and we've got mean, variance, and stdev..
Some Theory for those interested
-
The calculation above is a pure 'second moment' calculation, summing the
squared
differences and dividing by N. Why is Attaway's formula different,
dividing
by (N-1)?
-
For reasonable size N it doesn't make much
difference. The problem is that in a statistical (not physics)
context, we are trying to estimate a number that represents an entire data
population of whom we have only seen N samples (our N data points).
We are not allowed to count samples twice; that would bias (shift)
the answer. If we added the mean μ in as a sample, that would
decrease the variance (since N would go up). But the mean tells us
nothing
new about the samples: in fact from the mean and any (N-1) samples we
can re-construct the "missing" Nth sample.
-
BUT we use the mean μ in calculating the variance. AND we use all
N of the data points too. We're clearly counting something twice, and
to offset the resulting biased (too low) estimate of variance, we
should divide by the number of independent data points we are
entitled to: since μ is functionally equivalent to a data point,
we are now only entitled to say we have N-1 points for the variance
computation,
given the mean.
-
Matlab's
var(), std() built-ins compute the statistical (normalized
by N-1) version, but each has an extra argument that causes the
2nd-moment version to be returned.
-
For more on this topic, see the Model-Fitting lecture, which includes
a general formula analogous to the "fast computation" version of the 2nd
moment.
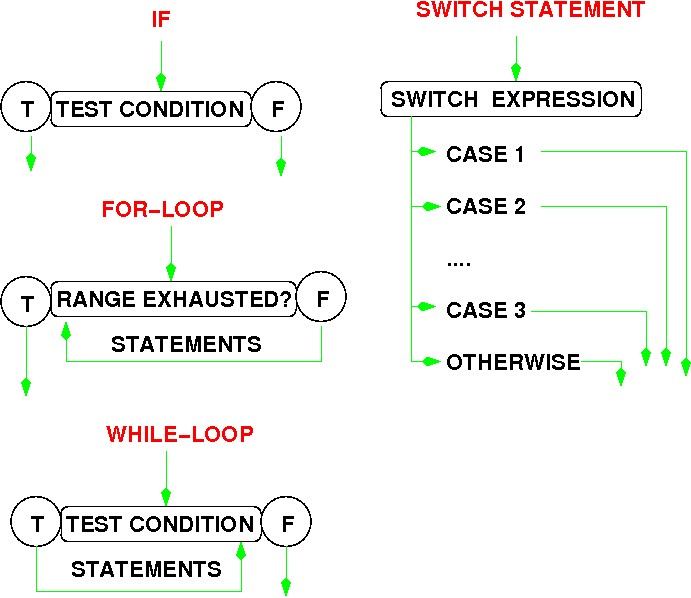
CONTROL SUMMARY
Almost always, one of these statements is best for what you want to do.
- IF : Depending on a single test
(condition)
you do either one action or another.
- SWITCH : Multi-branch version of
IF .
Depending on which of
several
CASE
values a test variable has, do the appropriate one of several actions.
- FOR : Do a particular set of
commands
a known number of times.
- WHILE : Do a particular set of
commands as long as, or until, a single condition is met.
FLOWCHART FRAGMENTS
Vectorized Commands and 1-D indices
Destroy before reading or read and forget! This is very ugly
stuff!
For some simple tests, Matlab has a vectorized version,
which unfortunately uses a form of indexing where matlab pretends
an n-dimensional matrix is really a long 1-D vector (matrix written
out columnwise). We've seen this weirdness before when we put a 2-d
matrix in as the 'range' in a for-loop.
The following is for your horrified amusement only.
We do not recommend knowing about, let alone using, this
confusing nonsense.
>> a = magic(3)
a =
8 1 6
3 5 7
4 9 2 % magic square
>> g5 = a > 5 % employ matrix form of >
g5 =
1 0 1
0 0 1
0 1 0 % a binary matrix
% Treat relation as index!
>> a(a>5) % same as a(g5)
ans =
8
9
6
7 % returns values > 5 in a column
>> find(a>5) % returns indices of values >5
ans =
1
6
7
8
% BUT they're the 1-D form of indices!
Over to You and Attaway! Read Chapter 5.

Last update: 04/22/2011: RN



