
If we only have the function defined at discrete points (say it's a vector of experimental readings, or the output of Matlab's differential equation solver, for instance), that brings in the issue of interpolation, an important numerical technique we'll ignore for now.
You may have seen this root-finding method, also called the Newton-Raphson method, in calculus classes. It is a simple and obvious approach, and is an example of the common engineering trick of approximating an arbitrary function with a "first-order" function -- in two dimensions, a straight line. Later in life, you'll expand functions into an infinite series (e.g. the Taylor series), and pitch out all but a few larger, "leading" terms to approximate the function close to a given point.
As usual, Wikipedia has a very nice article (with a movie), on Newton's method. For the mathematically inclined there's a proof of the method's quadratic convergence time: roughly, the number of correct digits doubles at every step. (BTW, the proof uses a Taylor series.)
The Idea:
Considered as an algorithm, this method is clearly a while -loop; it runs until a small-error condition is met.
The Math:
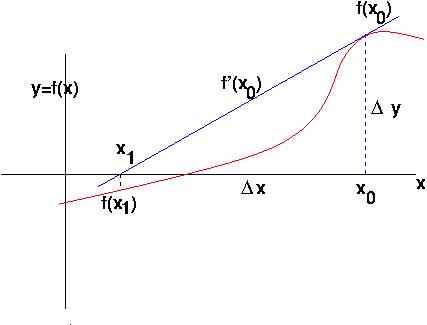
Say the tangent to the function at
Repeat until done: Generally,
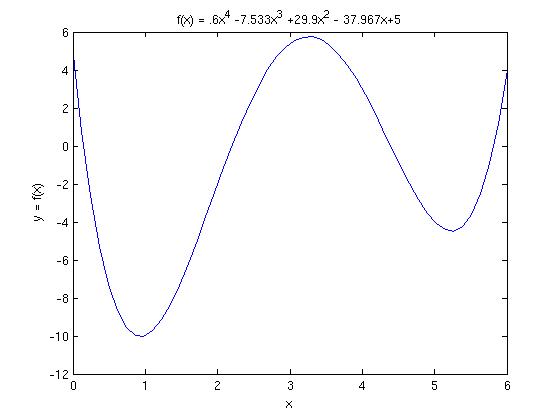
Example: The function
We can see there is a root near 4.4, for instance.
3 iterations of the method starting at
CB's function [my_root, err] = newton(x0, maxerr)
is 11 statements long, including 2 to count and print iterations and 2
to assign a global array of polynomial coeffficients.
the functions function y = f(x) and der = f_der(x)
are four statements, including function, global, end, and one
line
that actually does some work.
Extensions and Issues: There are lots of extensions, and various tweaks to the
method (use higher-order approximation functions, say). The
method extends to functions of several variables
(i.e. higher-dimensional problems). In that case it uses the
Jacobian matrix you may see in vector calculus, and also the
generalized matrix inverse you'll definitely see in the Data-Fitting
segment later in 160.
Clearly there are potential problems. The process may actually
diverge,
not converge. Starting too far from the desired root may diverge or find some
other root. See a more in-depth treatment (like Wikipedia, say)
for more consumer-protection warnings. To detect such problems and
gracefully abort, One could watch that the
error does not keep increasing for too long, or count iterations and
bail out after too many, etc.
Here's Wikipedia:
Secant
method.
The Idea:
The Math: Easy to formulate given we've done
Newton's method. Starting with Newton (Eq. 1), use
the "finite-difference" approximation:
Generally,
Example:
For the same problem as above, a reasonable function prototype is
Extensions and Issues:
The most popular extension in one dimension is the method of false position,
(q.v.)
There is also an extension to higher-dimensional functions.
Same non-convergence issues and answers as Newton, only risk is
greater with the approximation.
The convergence rate is, stunningly enough,
the Golden Ratio
, which turns up all sorts of delightfully unexpected places, not just Greek
sculpture, Renaissance art, Fibonacci series, etc. Thus it is
about
1.6, slower than Newton but still better than linear.
Indeed, it may run
faster since it doesn't need to evaluate the derivative at every step.
(Eq. 1)
Secant Method
The Background: Same assumptions as for Newton, but
we use two initial points (ideally close to the root) and we
don't use the derivative, we approximate it with the secant line
to the curve (a cutting line: in the limit that the cut grazes the
function we have the tangent line). The secant line concept is not
immediately obviously related to the trigonometric secant
function. The
secant method has been around for thousands of years.
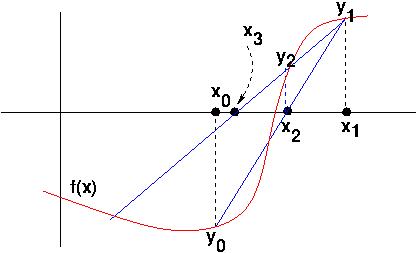
This is the same while -loop
control
structure as Newton, but needs a statement or two's worth of
bookkeeping since we need to
remember two previous
Thus for the secant method we need two initial
(Eq. 2)
function [my_root, err] = secant(lastx,x, maxerr).
Initializing at
Last Change: 9/23/2011: CB