Simulation & Design
Your Assignment
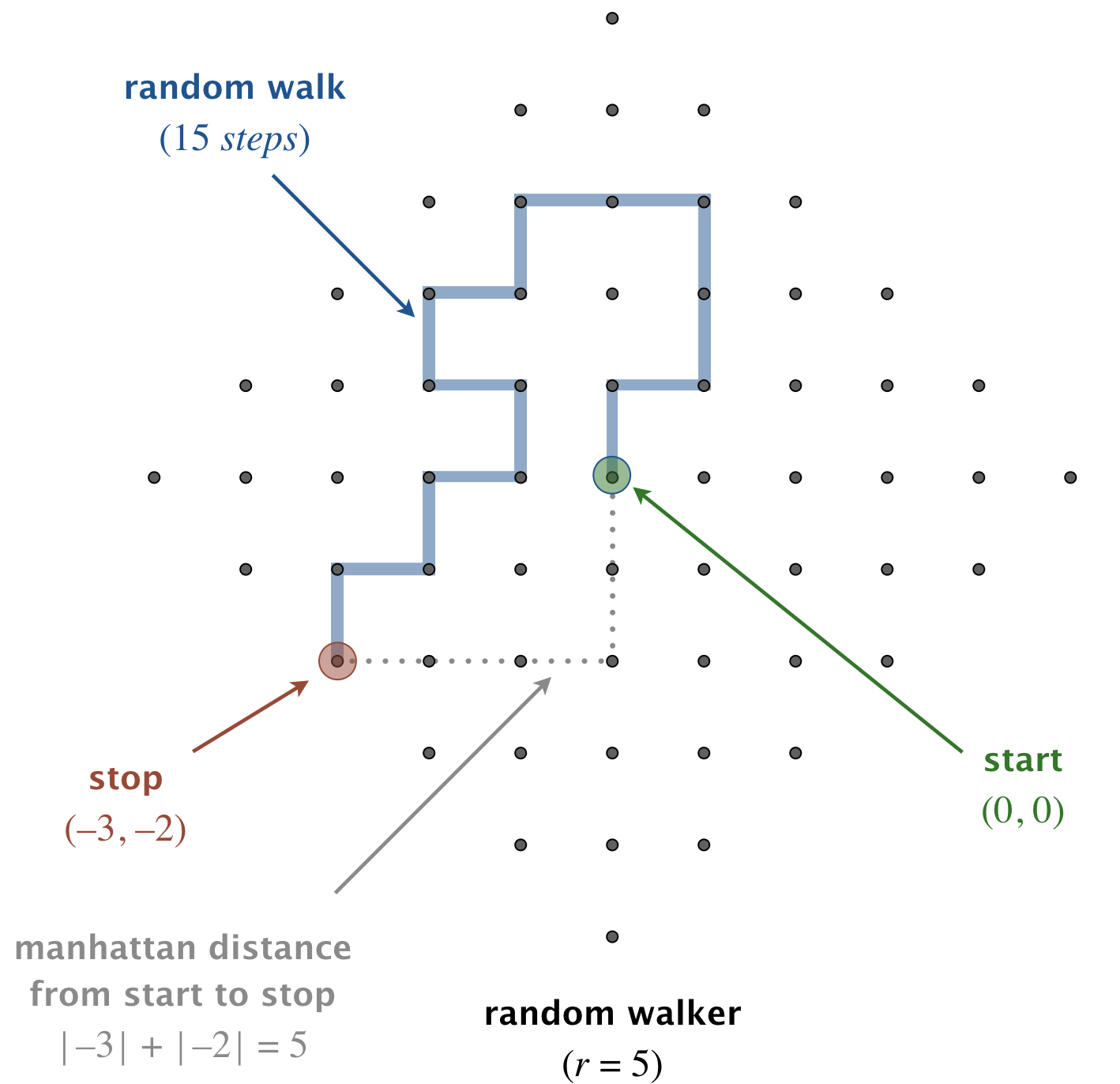
Consider you are standing at a street corner, in a city where the streets are laid out in a very regular grid pattern. At this point you randomly choose and intersection to turn on to (up, right, down, or left - let’s say). You walk further to another intersection and make the same random choice. Rinse, lather, repeat. When you finally stop, your winding path is some direct distance away from your starting point. This is an example of a random walk. It’s a probabilistic simulation of certain statistical systems (like photons inside a star, or Brownian motion of molecules).
In n steps, how far do you expect to be from your starting point? Write a program to help answer this question.
The requirements for this assignment are as follows:
You will need to use function(s) from the Python
Because we are using random numbers, in order for your output to match the example you must follow the following steps!randommodule.- At the beginning of your program (the first line in main), write:
random.seed(0) - When you are picking a random direction, use random.random() and
- Interpret a value less than .25 as moving UP (increase y value by 1)
- Interpret a value greater than or equal to .25 less than .5 as moving RIGHT (increase x value by 1)
- Interpret a value greater than or equal to .5 less than .75 as moving DOWN (decrease y value by 1)
- Interpret a value greater than or equal to .75 less than 1 as moving LEFT (decrease x value by 1)
- At the beginning of your program (the first line in main), write:
Your
mainfunction will be used to ask for user input and perform m number of walks.You will write a function called
random_walk_2dthat will perform a random walk of n steps. The function’s signature (its defined parameters, and return values) are to be designed by you.
The distance from your end point to your starting point is the Manhattan Distance, or the minimum number of steps to get back to the origin (see the picture).
Output
Because random processes are involved, your results may vary, but the output should look like the following example runs.
A simulation of 3 different walks, each taking 45 steps:
How many walks should I do? 3 How many steps should I take on each? 45 Average distance from start: 10.33
A simulation of 50 different walks, each taking 1000 steps:
How many walks should I do? 50 How many steps should I take on each? 1000 Average distance from start: 37.52
Note: All printed strings must match the above output. To otherwise deviate will not pass the autograder.
Average distance will be formatted to 2 decimal points.
Submission Requirements
The title for this lab is hw8. Your submitted file is
required to be named hw8.py.
Grading
The rubric for this assignment is available through Gradescope. An abbreviated version can be found here.