CSC 162 Four-coloring Project

Spring 2010

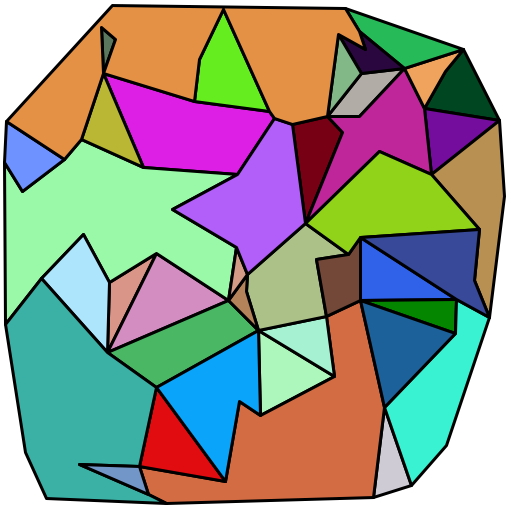
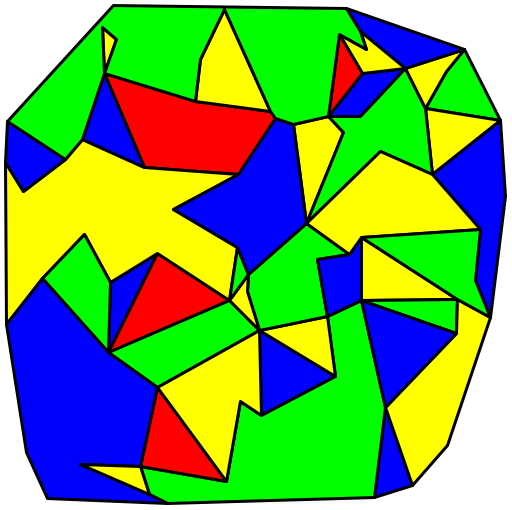
Imagine a map in which countries (or states, or counties) are rendered in contrasting colors, with no two neighboring countries the same.  What is the minimum number of colors required to create such a map?  Some maps can be colored with only 2 or 3 colors.  It turns out that any map with contiguous (one-piece) tiles can be colored with no more than 4 colors.  This perhaps surprising fact was first suggested in 1852, but not proven until 1976 (with the help of a computer program that worked out more than a thousand base cases). 

We can find a four-coloring for an arbitrary map via exhaustive search:  enumerate all the possible colorings and check each one to see whether any adjacent tiles are colored the same.  Again perhaps surprisingly, there is no known technique that is fundamentally faster than this—and in fact there cannot be, unless the P=NP conjecture (the most famous open problem in computer science) turns out to be true, which pretty much no one believes.  For more information (if you’re curious), check out the article at Wikipedia. 

Fortunately, most maps have a lot of possible four-colorings, and even exhaustive search tends to come up with one of them up pretty rapidly.  For this, the second programming project of the semester, we are providing you with starter code that generates random maps (rather pretty ones, if I do say so myself), which you must then four-color.  You’ll do so using recursive backtracking, a form of exhaustive search.  As in the first project, the amount of code you will need to write is very small.  Feel free to brainstorm with classmates, but please write your own individual code. 

Details

The program that generates maps is written in Java.  You’ll need to have Java (version 1.5 or newer) installed on your machine in order to run this program.  If you don’t have Java, you can get it from java.sun.com for Windows or Linux, or from apple.com/java for Mac OS.  If you double-click on the Map.jar file, it will display a window in which you can cycle through pictures.  You can try it out in your browser by clicking HERE.  You can also run it from a command-line shell or from a Python program.  These latter options allow you to specify command-line arguments that tell the program to gnerate a single map and print it out (in the form of a bunch of numbers) instead of drawing a picture. 

The Python starter code we’re giving you uses the print-it-out option, through a somewhat cryptic invocation of the Popen function from the subprocess module.  You needn’t worry about how this call works.  Its effect is create a file object, MAP, from which to read the output of the Java program.  That output consists of

1. A header line that echos the command-line parameters.  This is useful if you save the output to a file and want to remember where it came from, but you can ignore it for this assignment. 

2. A line that begins with the number of tiles in the map.  You need this.  Let’s call it M.  The other four numbers on the line are the minimum and maximum X and Y coordinates of points in the map; you can ignore these. 

3. M pairs of lines—one pair for each tile.  The first pair is for tile 0; the last pair is for tile M−1.  Within each pair, the first line comprises a series of pairs of numbers that specify the X and Y coordinates of the points on the outside perimeter of the tile.  The second line comprises a list of the neighbors of the tile—the tiles with which it cannot share a color. 

If that all seems a little daunting, rest easy:  the Python starter code reads all of this in and uses it to create a data abstraction—class Map—that you can use directly.  When you create an instance of this class,

    m = Map()

When you start up the program, you’ll find that it immediately (well, after a brief pause) displays an initial map.  If you click on the map twice (pause a little between clicks) it will display another map.  The first click causes the program to execute method Map.fourcolor(), which is currently empty.  The second click causes the program to create a new map.  As in the previous assignment, the starter code uses the simple Zelle graphics.py module; you’ll need a copy of this in a place where Python can find it.  To end the mouse click cycle, type ^C (control-C) in IDLE’s console window.  To start again, call run(seed), where seed is an arbitrary integer that determines which picture you’ll start with. 

Your job is to implement Map.fourcolor() and whatever else it needs to call.  You’ll probably find it helpful to do most of the work in a recursive method in class Tile.  I’ve left a placeholder for this, with a few suggestions in a comment; take a look.  The total amount of code you’ll have to write is quite small, and will strongly resemble what we did in class for the water-jug problem. 

Reminder

Please read the grading standards web page carefully and follow its instructions.  In particular, note that you will need to create a README.txt or README.pdf file, and you will need to turn your code in using Blackboard. 

Extra Credit Suggestions

For extra credit (counted at the end of the semester; may raise your final grade), you might consider the following possibilities. 

• Switch to a better graphics package (one that never leaves the window unresponsive). 

• Experiment with different parameters to Map.jar: 

  -n  num

  sets the total number of points in the map

  -m  num

  indicates the desired number of tiles (there may be fewer, if the number of points is too small)

• Implement a heuristic (a rule of thumb that usually works well) to increase the likelihood of finding a four-coloring soon.  One suggestion:  sort the tiles from largest to smallest number of neighbors, so you start coloring with the tiles that are most likely to have a lot of conflicts.  Given a list L, the command

      L.sort(key=functionName, reverse=True)
  

  will put the elements of L into reverse order, where functionName is the name of a function (perhaps one you wrote yourself) that inspects an element and returns a value on which to sort (like the number of neighbors, if the element is a tile). 

Due Date:  Tues., Feb. 23 at 12:00 noon; no extensions.

Last Change:  22 February 2010 /