You are to write a properly synchronized multithreaded program to solve
the traveling salesman problem (TSP).
You may work in teams of 1, 2, or 3.
You may write your code in any language that can interface properly to
the Solaris or pthreads library. C or C++ are probably
easiest.
Given an undirected graph with edge costs, the problem is to find the least cost tour (path) in a graph of N nodes that visits every node exactly once and ends at the same node at which it started. As most of you know, the problem is NP-complete, so you won't be solving very big instances: maybe 15 nodes.
Your program must read an ASCII file as input, either from a file
specified on the command line or, if none is specified, from standard
input. It must also accept a -t N (or -tN)
command line switch that tells it to create N threads. The threads will
then coorperate to find the cheapest tour in the graph. You should use
version of the thread creation calls that give each new thread its own
``LWP'' (kernel-implemented lightweight process).
The input file will contain the integer N, followed by (N2-N)/2 integers that constitute the upper triangle of the adjacency matrix of the graph. Your program must accept arbitrary white space separation between integers. It is important that you use this input format; the TA will be making test data available.
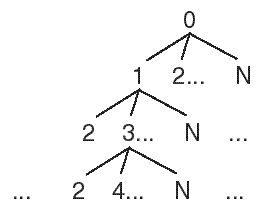
I suggest you solve the problem using a branch and bound algorithm. Think of the graph as defining a tree-structured search space, where every node of the tree represents a visited node of the graph, and the children of a node of the tree represent the nodes of the graph that might be visited next. Without loss of generality, assume we label the root of the tree node 0, indicating that our tour begins at node 0 of the graph. The root of the tree will have N-1 children, indicating the possible nodes to visit next:

The key to branch and bound is as follows. Suppose we keep track at each node of the tree of the cost of the path down from the root. If have already (in some other part of the tree) found a complete tour of cost C, there is no point in exploring portions of the tree below a node whose cost from the root already exceeds C. We can therefore prune that part of the tree.
Perhaps the simplest way to parallelize the search is for the initial thread to explore the tree down to level 3 or 4 (at which there will be about N2 or N3 nodes), and to place these nodes in a queue. (Note that you won't be able to keep the entire tree in memory: just the portion(s) you're working on.) The initial thread then creates T worker threads, each of which repeatedly removes a node from the queue and fleshes out the portion of the tree beneath it. A global structure keeps track of the cheapest tour found so far by any thread. Both the queue and the cheapest tour stucture require synchronization for concurrent access.
You may use either the threads or pthreads
library to create and synchronize threads. The pthreads
interface is a Posix standard; code that uses it is portable across a
wide variety of systems, including NT and all variants of Unix. The
threads interface is Solaris-specific, but a bit simpler
and reputedly (on Suns) a little faster. The two kinds of threads are
interoperable, and both are documented on the threads man
page.
For 256 you are not required to run your code on a multiprocessor, but you are required to write code that would run correctly on a multiprocessor if you tried it. Interestingly, you may discover that your multithreaded program runs faster for some values of T > 1 than it does for T = 1, even on a uniprocessor. This is because the multithreaded program explores the search space (tree) in a different order than the sequential algorithm does, and may (by sheer coincidence) discover a very low-cost path earlier than the sequential algorithm does, allowing it to prune the tree more effectively.
In addition to completing the 256 assignment, you are to run your code
on a multiprocessor (aorta.cs.rochester.edu), experiment
with a variety of program parameters, and attempt to maximize parallel
speedup. Specifically, you are to vary the level of concurrency T, the
level of multiprogramming (threads or processes per processor), and the
type of synchronization.
For synchronization, you must try at least the following four
alternatives: (1) the mutex objects of the
threads or pthreads library, (2) test-and-set
spin locks, (3) spin-then-wait locks, and (4) lock-free synchronization
based on compare-and-swap. You may want to look at the
following documentation from the SPARC v9 Architecture Manual:
Test-and-set
instruction (actually LDSTUB:
load-store unsigned byte)
Compare-and-swap
(CAS) instruction
MEMBAR
instruction
CAS are new in version 9 of the SPARC instruction set.
You will therefore need to compile your code with cc,
rather than gcc, and you'll need to specify the
-xarch=v8plus and -mt command-line switches to
the compiler.
You may also want to look at Maged Michael's concurrent queue algorithm. For lock-free access to a multi-word variable (e.g. the structure describing the best known tour), consider accessing the structure through a pointer, and using compare-and-swap to ``swing'' the pointer from an old value to a new one. (This technique is due to Maurice Herlihy [ACM TOPLAS Jan. 1991]). Beware of the ``ABA'' problem: if you read the pointer, create a new tour description, and then discover (in CAS) that the pointer has the value you read before, you need to know whether the data to which the pointer points has changed. The standard solution is to use a double-word CAS that changes both the pointer and a ``number of changes'' counter. You can see this solution in Maged's pseudocode.
The level of multiprogramming on a processor depends both on the number
of threads in your program and the number of unrelated processes on the
machine at the same time. Ideally, you would want to
run your final timing experiments when nobody else is
using the machine, so more or less all of the
activity on the machine would consist of programs you started yourself.
This may not be feasible, given concurrent use by the computer vision
group, so use the uptime and ps to get an
estimate of how much else is going on.
Multiprogramming is related in an important way to synchronization: if a
thread is preempted while holding a lock, no other thread can access the
protected data until the preempted thread is rescheduled. Intuitively,
you would probably expect that spin locks would cause the most serious
problems in this regard, and that spin-then-wait locks and lock-free
data structures would ameliorate the problem. Do you find this to be
the case in practice? How does scheduler-based (mutex)
synchronization compare?
Your turned-in README file should contain the results of your experiments, with clear presentation and explanation. Be sure to explain not only what happened, but why.
By the date shown below, send e-mail
to cs456 containing answers to the following questions:
pthreads
interface but not in the Solaris threads interface.
stdio library is thread-safe, so that
each call to printf occurs atomically.
 Back to the assignments and grading page
Back to the assignments and grading page