
Programming Concepts: Scripts and Functions
(Attaway Chs. 2, 5)
Syntax and Reserved Words
Most programming languages have reserved words, which
cannot be used for variable names and make up part of the
syntax of the language.
For example:
case = 9.34 * MyVar
is bad syntax for an assignment statement because
case is a
reserved word.
Important to understand in reading any programming language
reference book which parts of a statement are shown exactly as
they must be written (reserved words),
and which parts you are free to change.
ATTAWAY OBSCURES THIS CRUCIAL ISSUE! Authors usually write
reserved words in a
different typefont or color. Our book shows them looking the same
as function names or variables.
In our overheads, we'll (try to) use a distinctive color
or emphasis (or both)
to set off reserved words thus.
-
Example reserved words:
function end if else for while switch case break continue return otherwise...
- Statements like
if (selection) and
for (looping) use
reserved words in a particular grammatical way.
- Use lower case for reserved words; Matlab will cope if you don't,
but will complain.
- Best to treat built-in functions names
(e.g. sqrt, sin, sum...)
as reserved words to avoid confusion.
- MatLab help uses upper-case for reserved words.
- Attaway presents these reserved words, mixed in with function names,
at the end of the chapter where they're introduced in the "MATLAB
Functions and Commands" box.
-
Don't assume you need to quote anything if you don't see quotes
in the book examples.
Generally we only use quoted strings if we are printing
them or if we must send them into functions:
disp('Happy Birthday!');
plot(X,Y, '-r');
Note that we are treating the predefined function names
disp and plot
as reserved words.
Scripts (Attaway 2.2 - 2.5)
A script is a sequence of executable Matlab commands
that are stored in a file with a name like myscript.m
The .m suffix specifies that the file contains Matlab code.
The name myscript becomes an alias for the sequence of
statements in the file.
For example, if the file myscript.m contains the lines
a = 5;
b = 6;
c = a + b;
then typing
>> myscript
at Matlab causes variables a, b, and c
to be defined, and to take on the values
5, 6, and 11.
Note that because of the semicolons following each line,
Matlab does not print out any intermediate responses when the script
is invoked.
This scripting ability is staggeringly useful if you ever
want to issue a sequence of commands more than once.
You have created a stored program that allows a complex
sequence of operations to be invoked with a single command.
Properties of Scripts
-
All variables in the Matlab workspace are available
to any script called in the command window, and that any variables
defined in a script appear or are redefined in the workspace.
This can be useful, but also makes it easy to get confused about
what various variable names
refer to if there are very many scripts being used in a particular session.
-
A script file is a text file, and can be created using any editor
text editor. In Matlab, clicking new and then script
under the file pulldown menu will invoke the Matlab editor,
and alow you to type a script in the edit window.
You will have to save it and give it a name.
-
The contents of a script known to Matlab can be displayed in the command window
using the type command, e.g.,
>> type myscript
User-Defined Functions (Attaway 2.7, 5.1)
Because of the potential for confusing names and
unexpected interactions when using scripts,
Matlab provides a more circumscribed mechanism for chunking
commands together in useful blocks.
This mechanism is the user-defined function.
You can write your own
abs()
function or a brand-new function useful in your problem.
Your function can take or return any number of arguments, or even a
variable
number of either, but we'll start with one returned value.
Function Definition
Each function must be defined before it is used.
For example, suppose we want to create a function called
my_func,
- Using an editor (Matlab's is good), create a file in the
Matlab directory called "my_func.m".
- First line is the function prototype,
(or header), for your function
with name "my_func".
- Next few lines are comments describing inputs and outputs.
- Then comes the function body: matlab commands executed when
the function is called, including possibly other function calls.
- Generally these lines are terminated with a semicolon ;
to suppress the output matlab would generate otherwise.
- The last line must be an
end statement.
In Matlab, from the File tab choose New (script or function). The
function choice gives a template that must be modified. The
script choice is blank.
User-Defined Functions (cont.)
The Function prototype is a standard form that
provides the name of the function,
the number of arguments (inputs) and the names that will be used to
refer to those arguments inside the function definition, e.g.,
function return_val = fun_name (arg1, arg2,...)
When the function is called (used, invoked) with the arguments,
it evaluates to (returns) the return value (usually depending on the
arguments).
So, for example...
function sum_ans = Sum3(a,b,c)
% returns sum of three arguments
sum_ans = a + b + c;
end
or
function C = fahr_to_cel(F)
% converts degrees Farenheit to degrees Celsius
C = ( 5/9) * (F - 32);
end
NOTE CAREFULLY: The function uses the arguments
to compute its answer and assigns the answer to the
return-variable.
When you have written your function, save it
(if you used the "new script" menu selection, you need to provide a name
that is the same as the function name.
For "new function", the name of the
function is suggested automatically as the file name to use).
Using Functions
Function call: To use the function, your code must mention the
function name, provide actual arguments and
capture returned value(s), just as with built-in functions, e.g.,
% built-in
>> Sqrt2 = sqrt(2);
>> some_sqrt = sqrt(5 + sin(.44));
% written by me
>> freezing_cel = fahr_to_cel(32);
>> my_sum1 = Sum3(1,2,3);
>> my_sum2 = Sum3(10, 20, 30);
The values you want to apply a function to (arguments) can be in variables.
>> x1 = 45;
>> x2 = sqrt(132);
>> x3 = x2 * pi;
>> My_sum = Sum3(x1, x2, x3)
>> Fdeg = 93;
>> Cdeg = fahr_to_cel(Fdeg);
Programming Languages aren't Spreadsheets
Consider the following:
>> x1 = 45;
>> x2 = 10;
>> x3 = pi;
>> My_sum = Sum3(x1, x2, x3)
My_sum = 58.1416
>> x1 = -99;
>> My_sum
My_sum = ?????
Has My_sum's value changed? NO!
It keeps its value until we re-assign or clear it. Assignment is not
mathematical equality in Matlab (or C, Fortran, Java, C++, LISP, Python...).
Maintaining consistent mathematical equality is what you pay a
spreadsheet
like Excel® for, and why its inventors got rich.
Super-good idea:
Excel 'cells' have a (column, row) address like A1 or B3. A cell
holds a number, possibly computed by a (hidden) formula in the cell,
like a little function call. Excel's job is to keep all the numbers
in all the cells consistent. Below, C1 has a formula, "the sum of
cells A1 and B1"). If I change A1 or B2, C1 changes!
A B C
1 45 -90 =(A1+B1)
2 =(B2+1)
Note that I can't assign a number to C1 without losing the formula and severing
the (mathematical equality) dependence between the three cells.
Therefore the formula in row 2 must be (and is) a spreadsheet error. It is
like writing x = x+1 in math, which
is either crazy, a flat-out contradiction, or an 'infinite loop'.
On the other hand in programming we correctly write things like
x = x + 1;
all the time! The difference is that in Matlab this assignment is
something
to be executed once. It's NOT a condition to be maintained.
Functions: Idea and Consequences
Function user should have to know only the minimum about
a function to use it.
- Its meaning: What it computes from what. (Its inputs and outputs).
- Its name
- The particular number, order and type of input arguments.
- And for Matlab, The number, order and type of outputs
The function user does not need to know details about the code that
implements the function,
specifically not the internal names used.
We don't know what
names are used inside Matlab's implementation of sqrt(),
and we don't care.
The whole idea is that after we have a working function
(written by us or by a co-worker on a group project, say), we can
happily forget
most of how we or she did it, especially the internal names we used!
Room analogy: a function is an environment, like a room, with its own
chests of labelled drawers (variables). Calling a function is like
going
into another room, where you might
find the same labels but they're on different drawers!
Functions: Specific Points
-
The name of function and number,
order, (and generally type) of arguments and output in call
must be same as in function definition (prototype). This is the
function's "public face", its interface to the world. This is all
a user needs to know.
- Value of definition's return-variable is returned as function's
value
when function is done computing.
-
Names of arguments can differ between function calls and
definition, or they can be the same. The function-caller does not
(need to) know or care what the function-writer wrote!
-
Likewise, the
name of the function-caller's
variable receiving the function's return value can differ from
function definition's return variable name, or it can be the same.
Again,
the function-caller does not
(need to) know or care what the function-writer wrote!
function ret_val = BobFn(arg1, arg2)
% above is the first line of a function definition
% the definition lives in a file called BobFn.m
Freddy = BobFn(A(1), -87);
% above is a call to BobFn.
% Only the function name is (must be)
% the same between the call and the definition.
Functions: Recap
Functions and Scripts: A script is a sequence of statements
executed at the command level. It's unnatural and unusual to call a
script within another one. It can ask for user input but cannot take
arguments. It can print and assign but it cannot return values.
A function is a useful piece of code that usually accepts arguments,
computes with them, and returns an answer -- the function expression is
evaluated (in the function body, using the arguments)
and the result is substituted into the program
that called the function at that place.
Programmers often nest function calls since problems often fall apart
into almost-independent sub-parts.
Functions provide a way to structure your code and abstract useful
functionality, just as built-in functions do. E.g.,
elt_total = sum(sum(My_Mat));
Euclid_dist = sqrt(sum( (a - b) .* (a - b)));
Sum3(x(1), y(20,20), pi)); % user-written
To browse all available MatLab functions (!) use the small "fx" icon
in the lower left corner of the command window.
For details on using a built-in function, use
>> help function-name
For more detail click the
on-line help link. Use Matlab help.
What Often Goes Wrong
-
Bad syntax: the first line of the function file MUST look like:
function ret_val = Func_Name(arg1, arg2,...)
Don't put the function name before the =, remember that functions
almost always need arguments so there will be one or more variable
names in the parentheses, etc.
-
Functions mostly communicate with each other, not with humans!
A function does not need input from the user, nor must it necessarily print
anything. In fact that is rare behavior. Generally a function
communicates with a program or other function that calls it (thus
giving it 'input'), and receives the returned value as the function's
'output', e.g.:
Chill = Wind_Chill(Wind_Velocity, Temperature);
-
Function definitions are templates: don't get them mixed up with the
calling process. Below is misguided:
function ans = foo(x,y) %function prototype line
x = 3; % in function body
y = 5;
...
end
Above is misguided.
It compiles in particular values of the function's formal variables
and thus destroys the function's generality. Always think of needing
two
things: a function call and a function definition.
You can imagine the call at command-level and the definition off in
some .m file.
>> one_ans = foo(3, 5); % use foo w/actual arguments
% this call sets values of
%foo's formal arguments and runs it
function ans = foo(x,y) % in foo.m file
% define foo w/ formal arguments,
% does not execute foo.
-
You get a red error message to the effect that your function is undefined.
BE SURE you are in Matlab's working
directory! See the 'working directory' instructions from the
Files and Starting Matlab link on the main page or the
Working Directory directions for Assignment 1
- You get Matlab's red "undefined function" error message.
You may have named your function one thing
(like first_try and saved it: it will be in the file
first_try.m.
But then you went back and
edited the definition to give the function a different name like
exercise_1.
Saving this edit keeps the OLD name for the file, and so
invoking exercise_1(arguments) fails since Matlab does not
find a exercise_1.m file. You can rename the file, the
function, whatever. But the function and file names must be
consistent.
Pick a good name and stick with it.
Exercise:
In Matlab's editor, write and save a function (you pick its name) to
convert miles to meters: the single input argument is a number
of miles, the output value is the equivalent number of meters.
You can use the constants 100, 2.54, 5280, and 12. At command level,
use your function to get the
meters in a mile and the meters in a marathon.
When you are done, enter your answer for meters in a marathon
(to four decimal places) below. Just once, please.
See results
Calling Functions from a Script
In all future assignments, you'll be calling functions you write
from a script (called main.m). The script is the glue that
assembles your functions into a working program.
Not just the script, it's the names of variables that does
the gluing. Here's a typical script calling functions you've written.
% First, somehow get input data
Input_Values = Get_Inputs(); % or maybe
Input_Values = Get_Inputs(lo_val, hi_val); % or
Input_Values = Get_Inputs('file_name');
% Then apply your functions
Answers = Process (Input_Values);
Make_Beautiful_Plots(Input_Values, Answers);
On a more mundane level, for next few weeks we'll be making scripts
like:
% exercise 1
Ex_1_Func(0,0,0) % should return 0
Ex_1_Func(1, 3, 5) % should return -99
Ex_1_Func(pi, -99, 140) % no idea but should make sense
% exercise2
Func_2(43) % should return 42
...
Scripts should be mostly function calls with Very Little Else!
Local and Global Variables (Attaway 5.4)
Most variables in Matlab are local. They have meaning in
only one context. In matlab there are two main types of contexts:
- The command window has active variables shown in the workspace
window, and named (or described) if you type
>> who % variable names
>> whos % variable names and values
-
A .m file containing a function or a function and subfunctions,
only has access to variables declared as parameters, or defined in the file.
-
A .m file containing a script does not provide local context.
A script is always invoked (called) from some other context
(the command window, another script, a function)
and will share all its variables with the invoking context.
If these variables
were perhaps not meant to be shared... confusion results.
(One big reason we like functions better than scripts)
-
Locality means that changing the value of a variable in one context
does not affect variables in other contexts, even if they have the
same name.
The opposite of local is global. Since we usually want local
variables, and in fact globals are usually a bad idea, globals must be
declared as such by a command like:
global GLOB1 MYGLOB; % note no commas
Often global variable names are capitalized as a warning.
-
If two contexts both have a variable declared global, then they are
sharing it: if one changes it, it will change in the other.
-
In the room analogy, it's like there is a shared drawer
(maybe it's mounted in the shared wall with the same label on both
sides?.) Only it can be shared by any program that designates the
label (variable name) GLOBAL.
-
This is an easy way for the programmer to get mixed up, and is why globals
are generally bad.
Sometimes useful though (for "urgent message" variable) for instance,
or a variable that everyone shares, like "gravitational constant".
Variable Binding (Attaway 2.7.5)
This is a VITAL CONCEPT and people have trouble with it.
Be honest: if you don't get this, or have any doubts at all, read
more, try more experiments in MatLab, or talk to TA or prof.
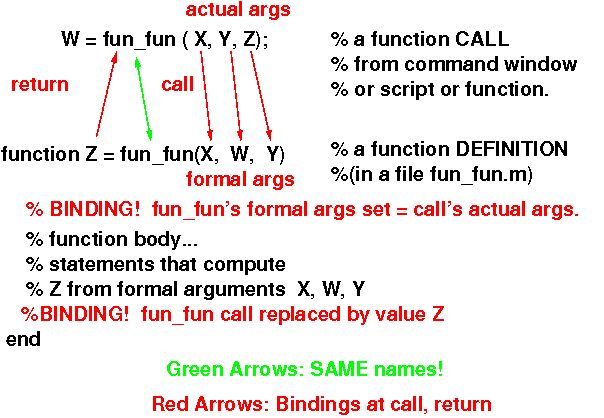
-
Function name must be the same in .m file, function definition,
and
function call.
- Names in function definition are local; they denote
DIFFERENT variables from any names in other functions, scripts,
or command window.
- Names may be spelled the same, but in context have different
denotations...
like thay had different "last names". Fred (Smith) ISN'T Fred
(Jones).
FRED (in command level or in function call) ISN'T FRED (inside
function).
- Function definition's formal arguments are bound when
function is called -- just like an
assignment,
body is executed with those bindings (values), then answer is returned
by binding the function definition's return variable to the variable
assigned to in
the function call statement.
Examples (Attaway 2.7)
Suppose we have defined a function in the file my_diff.m as follows.
function difference = my_diff(a,b)
difference = a-b;
end
In a script, or at command level, we can do the following
>> a_diff = my_diff(17, 2.2)
a_diff = 14.8
>> m1 = 5;
>> m2 = 7;
>> the_diff = my_diff(m1, m2)
the_diff = -2
>> a = 9;
>> b = 4;
my_diff(b,a)
ans = -5
my_diff(a,b)
ans = 5
A function call is OK as an argument
>> some_diff = my_diff(sqrt(25), 5))
some_diff = 0
So this also works!
>> another_diff = my_diff(my_diff(20, 10), 5))
another_diff = 5
Function Variants (Attaway 5.1)
Functions with no arguments:
Functions don't necessarily need input arguments, (don't
need their parentheses, either!)
(in the following examples, the built-in function
input does what you would think)
function ret_val = doubler
ret_val = 2 * input('number? ');
end
This is the same as
function ret_val = doubler()
ret_val = 2 * input('number? ');
end
And at command level they work the same:
>> doubler;
number? 4
ans = 8
>> doubler();
number? 7
ans = 14
Returning Multiple Answers (Attaway 2.7.5)
Matlab functions can return multiple values.
Here's an example for the quadratic formula:
function [root1, root2] = QuadForm(a,b,c)
% returns two x's for which ax^2 +bx +c = 0
% note: they may be complex numbers!
root1 = (-b + sqrt(b*b - 4*a*c)) / (2*a);
root2 = (-b - sqrt(b*b - 4*a*c)) / (2*a);
end
CAREFUL! Must explicitly name the variables for multiple
answers in the calling statement.
Rootvec = QuadForm(3.0, T2, F); will NOT work!
You'll get root1 assigned to Rootvec and lose
root2 altogether!;
[myroot1, myroot2] = QuadForm(3.0, T2, F); works
Variable Binding Surprise Revisit! (Attaway 2.7.5)
All variables in the function definition and body are NEW! They may have
the same names as variables in other functions, or defined in the
current
workspace, or whatever, but they are LOCAL: the formal argument
variables
are bound in the function call, and others are assigned
in the function execution, and they all totally vanish upon function exit.
The scope of a variable is that extent of code in
which it is defined (a 'context').
When a function is called (from a script or outer function)
the program leaves the scope of any local variables defined at the call point.
On return, all local values are intact.
Normally there is no way to change the value of a variable
at a "higher level" (say the command level) by
making a function call
(except by assigning it to the value returned by the function call). So
x = 10; % say we're in context A
y = 5;
z = -99;
x = my_function(x,y);
changes the value of x in context A,
but only in the same sort of way that x = x + 1 would.
Nothing hidden inside the function can change x or y in context A,
despite them being passed in as arguments.
In my_function's context, z's
(context A) value of -99 cannot be seen; consequently, the function
can use z as a local variable without affecting its value of -99 in
the function-calling context A.
More Naming and Scoping (Attaway 2.7.5)
Define a function:
function [x y] = Fred( u, v, w )
a = 1;
b = 2;
end
Here, notice that variables
a,b,u,v,w,x,y,z are ALL different from those in
any calling context, e.g
>> [u,v] = Fred(a,v,b)
Now here's a function call:
>> q = Hilda(5)
q = 24
What happened? With the definitions below, let's see:
function x = Hilda(y) % on call, y set to 5
z = 1; % z local to Hilda
x = Gerry(y+1); % Fn Call! (poor use for x)
% with y=5, Gerry returns 18
% local x becomes 18, z is still 1
x = x+z+y; % x is reset x = 18+1+5
end % Hilda returns x to caller
%---------------
function x = Gerry(y) % different x, new y set to 6
z = 3; % Hilda's z unaffected
x = z*y; % x = 3*6
y = pi; % other y's unaffected
end % returns x to calling context in Hilda
Demos 2
Demos 3
Subfunctions (Attaway 5.2.2)
-
Matlab HelpDesk
- Subfunction:
In the SAME .M file,
after a normal primary function definition,
subfunctions may be defined.
Subfunctions are only visible to
the primary function or other subfunctions in the file.
Variables are all scoped as with normal function operation, that is
neither the primary function nor the subfunctions can get at each
other's variables.
- Subfunctions are a way to keep intimately-related,
not-generally-useful
local functions with the functions that use them. They also
hide the structure and organization
and various subpieces of a
function from the caller.
Only the primary function name is available from outside.
function ... % primary function visible outside
...calls subfunctions
...
function %subfunction
end ...
function %subfunction
end ...
Optional: Nested Functions (Attaway 9.4)
Nested Functions: Actually define functions inside other
functions: one function's definition nests inside another function's
definition.
The scope of a nested function's
variables is the workspace of the outermost function where it is
defined.
The nested
function can access all the "nesting" function's variables, reducing
need for argument passing.
See Attaway or Matlab help for details.
function ... % primary function visible outside
... stmts
function %subfunction
stmts
function %subfunction
stmts
end ...
end ...
end
Finally, WHY FUNCTIONS? WHY NOT SCRIPTS?
Can have "sub-scripts", and can compute same things with functions and scripts BUT...
-
Every part of every script or sub-script can see all variables: they
are all global. This causes impossible confusion.
-
Makes team programming impossible: interfaces between chunks
difficult to describe, check, enforce.
-
Functions' private name-space allows free choice of names within
functions: they aren't confused with names in other functions or scripts.
- Functions compress important operations into one-line calls.
With script, no compression -- huge, impossible-to-read programs.
- Functions encourage creation of meaningful, reusable solutions to
sub-problems. Scripts don't.
Ultimate Extreme Scoping: Recursion
Attaway 2.7.5, 9.5
We get new names every time we enter the function. Seriously!
Even if it calls itself (recursion).
Here's the Wow.m file.
Achtung! Example below is first introduction to selection
statements, our next subject. As you see, the
if statement
is very easy to understand (reads like English).
Also the fprintf() built-in function
does what you would expect.
function Wow(x)
fprintf('\n into Wow with x = %d', x);
if x > 0
Wow(x-1);
end % end of if statement
fprintf('\n leaving Wow with x = %d', x);
end
And at top level,
>> Wow(4)
into Wow with x = 4
into Wow with x = 3
into Wow with x = 2
into Wow with x = 1
into Wow with x = 0
leaving Wow with x = 0
leaving Wow with x = 1
leaving Wow with x = 2
leaving Wow with x = 3
leaving Wow with x = 4
WOW! Note how a function always returns to the place it was called
from. So from
Wow with x = 0, the return goes back
to that version
of Wow with x = 1. The version
with x = 0 has no clue how far "above it" the original
call was: it can only return to its immediate calling context.
More Ultimate Extreme Scoping
Attaway 2.7.5, 9.5
Recursive definitions very common in math and CS: e.g.
n! = n* (n-1)!;
0! = 1.
fib(n) = fib(n-1)+fib(n-2);
fib(0) = 1,
fib(1) = 1
We see a rule for the general case, defined on smaller problem
with same function (recursive definition). We see a rule for
the base case(s), which is often simple and MUST ALWAYS BE REACHED
else we recurse forever.
Scoping rules mean we can write computer functions like the following.
function fact = my_fact(x)
% Idea is to notice, e.g.: 5! = 5*4*3*2*1 = 5*4!
if x <= 1
fact = 1; % answer for base case
else
% call (self) on smaller case.
% local x unchanged when my_fact returns
fact = x * my_fact(x-1);
end % end of if statement
end % end of function
Recursion is elegant, tricky to think about at first, very natural
when grokked (dated 60s slang, look it up).
Sometimes inefficient or wasteful. Fibonacci and
factorial more efficiently done with iteration ("for loop" -- our
next topic). In fact,
fib's "doubly recursive" nature means we compute
sub-answers multiple (exponentially many)
times, so it's a terrible mistake to try to
compute it this way!
So these are uncompelling functions to justify
recursion... they only illustrate it. BUT plenty of problems
where recursion is most natural and efficient approach.
Practical Recursion: Tree Traversal
4
/ \
/ \
1 7
/ \ / \
5 3 8 \
/ \ \
6 1 9
/ \
9 2
Here's a schematic diagram of a binary tree with a root with
value 4, nodes with values.
Every node has at most 2 "subtrees".
So a tree is a node (hmmm... a base case?) and subtrees
(smaller trees). Sounds like recursion!.
In fact, this "tree" represents a data structure that is DESIGNED
for recursion.
The only
things we can do with a node are print its value and find its left and
right subtrees (can be null).
Problem: given the root, print out every value. No information
on how big
tree is. Also, say the node values are totally random.
Note: Trees are a very common data structure: they can be used
to speed search for a matching value, and their rationale is the
subject of courses like CSC172 (Data Structures). Data bases,
indexes, and other very practical computing applications depend on them,
and they are conceptually useful in certain
real life applications. (How search a phone-book?).
Given our rules, if
we can search a sub-tree (which is a tree) we can search
a whole tree, so this problem is set up for a recursive solution,
which is made up of a base case and a general case involving
solving identical (but smaller) sub-problems. This is like
factorial but here recursion is an efficient and practical solution.
Pseudocode:
function print_tree(node)
print(value(node));
if node has left subtree
print_tree(left_subtree(node));
end
if node has right subtree
print_tree(right_subtree(node));
end
end

Last update: 04/22/2011: RN


