Newton-Raphson and Secant Methods

Newton's Method

The Background: If we know how to describe mathematically the scalar values x we want, we usually produce an equation describing them: "find x such that (equation in x = 0.)" Think of the quadratic equation, for instance: we need the x for which
a x² +b x + c = 0.

Thus the goal is to find a value of x such that our function of interest, f(x), is equal to zero. That value of x is a root of the function. There are as many (real) roots as places where the function crosses the x-axis. We assume the function is differentiable ("smooth") and that we can compute both it and its derivative

Newton and secant are examples of the common engineering trick of approximating an arbitrary function with a "first-order" function -- in two dimensions, a straight line.

Later in life, you'll expand functions into an infinite series (e.g. the Taylor series), and pitch out all but a few larger, "leading" terms to approximate the function close to a given point.

Nice article (with a movie), on Newton's method.

The Idea:

1. Guess an x₀ close to the root of interest.
2. Start Iteration: Approximate the function at that point by a straight line. The obvious choice is the line tangent to (in the direction of) the function's graph at that point.
3. Notice that the slope of the required tangent is the derivative of the function, so the line we want has that slope and goes through the point (x₀, f(x₀)) .
4. This tangent line goes through the x-axis at a point x₁, which is easy to calculate and which we bet is nearer to the root than x₀ is.
5. Compute x₁ and f(x₁), and we're ready to go to Start Iteration and repeat the process until for some x_i, we find a f(x_i) close enough to zero for our purposes.

Considered as an algorithm, this method is clearly a while -loop; it runs until a small-error condition is met.

The Math:

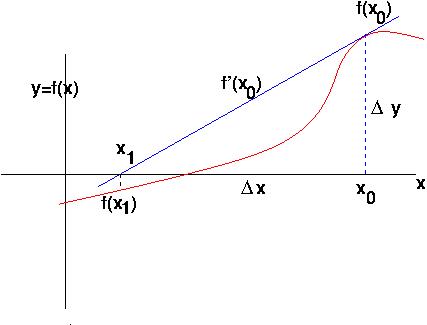
Say the tangent to the function at x = x₀ intersects the x-axis at x₁. The slope of that tangent is Δy/ Δx = f'(x₀) (where f' is the derivative of f), and Δy = f(x₀). Thus f(x₀)/(x₀ - x₁) =f'(x₀), and so x₁ = x₀ - f(x₀)/f'(x₀) . We know everything on the RHS and the LHS is what we need to continue.

Repeat until done: Generally,
(Eq. 1) x_i+1 = x_i - f(x_i)/f'(x_i).

Programming: Super simple: about 10 lines of Matlab, calling (sub)functions for f(x) and f'(x).

Extensions and Issues:

• Many extensions, and various tweaks to the method (use higher-order approximation functions, say).
• Extends to functions of several variables (i.e. higher-dimensional problems). In that case it uses the Jacobian matrix you may see in vector calculus, and also the generalized matrix inverse you'll definitely see in the Data-Fitting segment later in 160.

Clearly there are potential problems.

• The process may actually diverge, not converge.
• Starting too far from the desired root may diverge or find some other root.

To detect such problems and gracefully abort, One could watch that the error does not keep increasing for too long, or count iterations and bail out after too many, etc.

See a more in-depth treatment (like Wikipedia, say) for more consumer-protection warnings.

Secant Method

The Background: The secant method has been around for thousands of years. The hook is it does not use the derivative.

Same assumptions as for Newton, but we use two initial points (ideally close to the root) and we don't use the derivative, we approximate it with the secant line to the curve (a cutting line: in the limit that the cut grazes the function we have the tangent line).

Here's Wikipedia: Secant method.

The Idea:

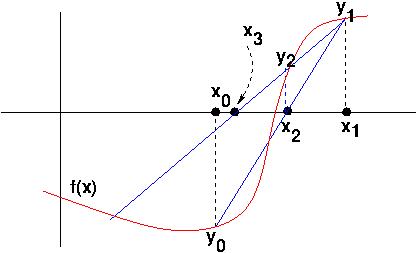
1. Pick two initial values of x, close to the desired root. Call them x₀, x₁. Evaluate y₀ = f(x₀) and y₁ = f(x₁).
2. As with the tangent line in Newton's method, produce the (secant) line through (x₀, y₀) and (x₁, y₁), and compute where it crosses the x-axis, and call that point
   x₂. Get y₂ =f(x₂).
3. Bootstrap along: replace (x₀, y₀), (x₁, y₁) with
   (x₁, y₁), (x₂, y₂) and repeat.
4. Keep this process up: derive (x_i, y_i) from
   (x_i-1, y_i-1) and (x_i-2, y_i-2) until y_i meets the error criterion.

This is the same while -loop control structure as Newton, but needs a statement or two's worth of bookkeeping since we need to remember two previous x's, not one. ( Do Not save them all in some vector, please! Always wasteful, sometimes dangerous, and no easier to write).

The Math: Easy to formulate given we've done Newton's method. Starting with Newton (Eq. 1), use the "finite-difference" approximation:
f'(x_i) ≈ Δy/Δx = (f(x_i) - f(x_i-1)) /(x_i - x_i-1).
Thus for the secant method we need two initial x points, which should be close to the desired root.

Generally,
(Eq. 2) x_i+1 = x_i - f(x_i) [( x_i - x_i-1) / ( f(x_i) - f(x_i-1))].

Extensions and Issues:

• The most popular extension in one dimension is the method of false position, (q.v.)
• There is also an extension to higher-dimensional functions.

Same non-convergence issues and answers as Newton, only risk is greater with the approximation. But it sometimes works better!

The convergence rate is, stunningly enough, the Golden Ratio, which turns up all sorts of delightfully unexpected places, not just Greek sculpture, Renaissance art, Fibonacci series, etc. Thus it is about 1.6, slower than Newton but still better than linear. Indeed, it may run faster since it doesn't need to evaluate the derivative at every step, or it may get lucky.

Simple-Minded Search

Step along until have two x values, l and h , such that f(l) < 0 and f(h)> 0. Then search in the interval [l,h] for an x such that f(x) is close enough to zero.

Binary search would be a good choice: as in "20 questions", idea is to divide the unknown space into two equal parts at each probe, so its size diminishes exponentially.

Find s, l : f(s) < 0, f(l) > 0 repeat m = (s+l)/2; if f(m) <= 0, s = m else l = m until f(m) <= max_error_allowed;