CSC 171 SPRING 1999
PROJECT # 2: GAUSSIAN ELIMINATION
ASSIGNED 3/15/99 – DUE 4/5/99
The example applet for Project2
Systems of linear algebraic equations arise in almost every aspect of engineering, applied mathematics, and scientific computation. Solutions of linear systems form the cornerstone for solving a wide variety of practical computational problems.
This project involves the programming two distinct modules.
Mathematical Preliminaries (Review)
Vectors
A vector with n elements can be thought of as a one-dimensional array of numbers. For example, the vector
1 2 3 4 5 6 7 8 9
Can be expressed as:
double vector1[] = {1, 2, 3, 4,5,6,7,8,9}; in the Java language.
Matrices
An m x n matrix (m rows, n columns) can be thought of as a two dimensional array of numbers. For example, the matrix
1 2 3
4 5 6
7 8 9
Can be expressed as:
double matrix1[][] = {{1, 2, 3},{4,5,6},{7,8,9}}; in the Java language.
Summation
We often find it useful to calculate the sum of a series of values. If the values are contained in an array, then a simple for loop is sufficient for summation.
In Java
double vector1[] = {1,2,3,4,5,6,7,8,9};
double sum = 0;
for (int I = 0;I<vector1.length;I++) sum += vector1[I];
Inner Products
We often find it useful to take the inner product of two vectors of equal length. The inner product of two vectors is the sum of the point-by-point products of their elements.
double vector1[] = {1,2,3,4,5,6,7,8,9};
double vector2[] = {10,20,30,40,50,60,70,80,90};
double sum = 0;
if (vector1.length == vector2.length)
for (int I = 0;I<vector1.length;I++) sum += vector1[I] * vector2[I];
Matrix Vector Multiplication
A matrix (A) expressed as a two dimensional array, can be multiplied by a vector (b) if the number of columns in the matrix is equal to the number of rows in the vector. The result is a vector (x) with the same number rows as the matrix. (i.e. Ab = x).
double matrix1[][] = {{1,2,3},{4,5,6},{7,8,9}};
double vector3[] = {10,11,12};
double vector4[] = new double[matrix1.length];
if(matrix1[0].length == vector3.length)
for(I=0;I<vector4.length;I++)
for(j=0;j<vector3.length;++)
vector4[I] += matrix[I][j] * vector3[j];
Matrix Matrix Multiplication
Matrix multiplication is defined as follows. A matrix (A) may be multiplied by another matrix (B) to generate a third matrix (C). This multiplication requires that the number of columns of A must be equal to the number of rows of B. The i-jth entry in the resultant matrix C is the inner product of the ith row of A and the jth column of B. It is important to note that in general order is important in matrix multiplication. AB != BA.
double matrixA[][] = {{1,2,3,4},{4,5,6,7},{7,8,9,10}};
double matrixB[][] = {{10,20,30},{40,50,60},{70,80,90},{100,110,120}};
double matrixC[][] ;
if(matrix1A[0].length == matrixB.length) {
matrixC = new double[matrixA.length][matrixB[0].length];
for(int I = 0 ; I < matrixC.length; I++)
for(int j = 0;j<matrixC[0].length;j++)
for(int k = 0; k< matrixB.length;k++)
matrixC[I][j] += matrixA[I][k] * matrixB[k][j];
}
Identity Matrix
The identity matrix (I) is an m-by-m matrix (square) with ones on the diagonal and zeros elsewhere. Multiplying any matrix by the identity matrix yields the same matrix (i.e. AI = =A). This can be verified by matrix multiplying the following matrices.
double matrixA[][] = {{1,2,3,4},{4,5,6,7},{7,8,9,10}};
double matrixI[][] = {{1,0,0,0},{0,1,0,0},{0,0,1,0},{0,0,0,1}};
Permutation Matrix
A permutation matrix is a square matrix with exactly one 1 in each row and column and zeros elsewhere (i.e. and identity matrix with its rows and columns permuted). Multiplying a permutation matrix P, by any matrix A will yield the same A matrix, with rows swapped.
Consider multiplying matrixP x matrixA if defined as follows:
double matrixA[][] = {{1,2,3,4},{4,5,6,7},{7,8,9,10}};
double matrixP[][] = {{1,0,0},{0,0,1},{0,1,0}};
It can be shown that the resultant matrix C will be {{1,2,3,4},{7,8,9,10},{4,5,6,7}};
Elimination Matrix
An elimination matrix is a matrix designed to annihilate all the entries below the kth position in a vector (or column of a matrix). If we start with a vector of length n and wish to annihilate all the entries in this vector past some index k. We can multiply an elimination matrix by the vector. The elimination matrix is defined as follows.
|
1 |
… |
… |
0 |
0 |
… |
… |
0 |
A1 |
A1 |
||
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
||
|
… |
… |
… |
… |
… |
… |
… |
… |
…. |
…. |
||
|
0 |
…. |
… |
1 |
0 |
… |
… |
0 |
Ak |
Ak |
||
|
0 |
… |
… |
-mk+1 |
1 |
… |
…. |
0 |
X |
Ak+1 |
= |
0 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
||
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
||
|
0 |
… |
… |
-mn |
0 |
… |
… |
1 |
An |
0 |
Where m = ai/ak, i = k+1,…,n.
Example
Consider the vector v1 = {2, 4, -2}. Multiplying the elimination matrix M1 = {{1,0,0}, {-2,1,0},{1,0,1}} times v1 yields the result vector r1 = {2,0,0}. Multiplying the elimination matrix M2 = {{1,0,0},{0,1,0},{0,0.5,1}} times v1 yields the result vector r2 = {2,4,0}.
Note that when ak is zero, the potential for a divide by zero error exists. The usual way to deal with this problem in a program is by swapping rows with a permutation matrix.
Gaussian Elimination
We can use the above mentioned matrix constructs to implement Gaussian Elimination in terms of matrix operations.
Consider the system of equations
2x1 + 4x2 + 2x3 = 2
4x1 + 9x2 – 3x3 = 8
-2x1 – 3x2 + 7x3 = 10
or in matrix notation (Ax = b).
|
2 |
4 |
-2 |
X1 |
2 |
||
|
4 |
9 |
-3 |
X |
X2 |
= |
8 |
|
-2 |
-3 |
7 |
X3 |
10 |
To annihilate the sub diagonal entries from the first column of A, we subtract two time the first row from the second row and add the first row to the third row.
|
1 |
0 |
0 |
2 |
4 |
-2 |
2 |
4 |
-2 |
||||
|
M1A |
= |
-2 |
1 |
0 |
X |
4 |
9 |
-3 |
= |
0 |
1 |
1 |
|
1 |
0 |
1 |
-2 |
-3 |
7 |
0 |
1 |
5 |
|
1 |
0 |
0 |
2 |
2 |
||||
|
M1b |
= |
-2 |
1 |
0 |
X |
8 |
= |
4 |
|
1 |
0 |
1 |
10 |
12 |
Now, to annihilate the sub diagonal entry of the second columns of M1A, we subtract the second row from the third row:
|
1 |
0 |
0 |
2 |
4 |
-2 |
2 |
4 |
-2 |
||||
|
M2M1A |
= |
0 |
1 |
0 |
X |
0 |
1 |
1 |
= |
0 |
1 |
1 |
|
0 |
-1 |
1 |
0 |
1 |
5 |
0 |
0 |
4 |
|
1 |
0 |
0 |
2 |
2 |
||||
|
M2M1b |
= |
0 |
1 |
1 |
X |
4 |
= |
4 |
|
0 |
-1 |
1 |
12 |
8 |
We have, therefore, reduced the original system to the equivalent (upper triangular) system
|
2 |
4 |
-2 |
X1 |
2 |
||
|
0 |
1 |
1 |
X |
X2 |
= |
4 |
|
0 |
0 |
4 |
X3 |
8 |
Or, expressed as equations
2x1 + 4x2 – 2x3 = 2
x2 + x3 = 4
4x3 = 8
The new system of equations can be solved by back substitution to obtain x = {-1, 2,2}.
(i.e. x1 = -1, x2 = 2, x3 = 2).
Back Substitution
Given a system Ax = b, where A is upper triangular we can always solve for x using the back substitution algorithm. The formal algorithm for this is defined below.
Simply:
xn = bn/an,n
xi = (bi – ( j=1 S i-1 ai,j xj))/a i,i
Simulation of a Physical System
The following diagram depicts a plane truss having 13 members (the numbered lines) connected by 8 joints, (the numbered circles). The indicated loads, in tons, are applied at joints 2, 5, and 6, and we wish to determine the resulting force on each member of the truss.
The example applet for Project2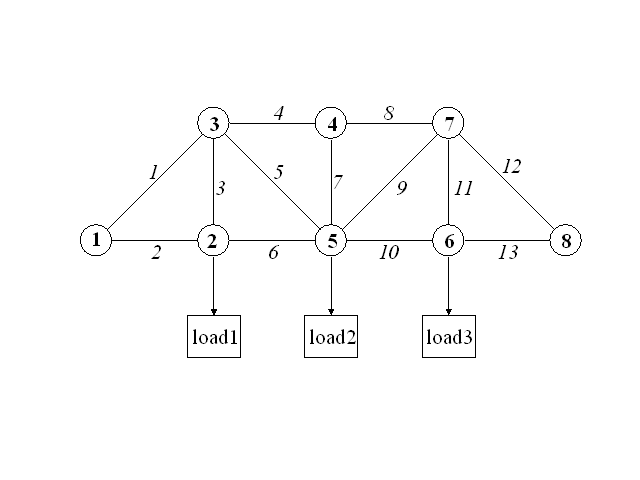
For the truss to be in static equilibrium, there must be no net force, horizontally or vertically, at any joint. Thus, we can determine the member forces by equating the horizontal forces to the left and right of each joint, and similarly equating the vertical forces upward and downward at each joint. For the eight joints, this would give 16 equations, which is more than the 13 unknown forces to be determined. For the truss to be statically determinate, that is, for there to be a unique solution, we assume that joint 1 is rigidly fixed horizontally vertically, ad that joint 8 is fixed vertically. Resolving the member forces into horizontal and vertical components and defining a = sqrt(2)/2, we obtain the following system of equations for the member forces Fi:
These equations can be expressed in matrix-vector notation as follows:
|
0 |
1 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
F1 |
0 |
||
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
F2 |
10 |
||
|
-a |
0 |
0 |
1 |
+a |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
F3 |
0 |
||
|
+a |
0 |
1 |
0 |
+a |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
F4 |
0 |
||
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
F5 |
0 |
||
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
F6 |
0 |
||
|
0 |
0 |
0 |
0 |
+a |
1 |
0 |
0 |
-a |
-1 |
0 |
0 |
0 |
X |
F7 |
= |
0 |
|
0 |
0 |
0 |
0 |
+a |
0 |
1 |
0 |
+a |
0 |
0 |
0 |
0 |
F8 |
15 |
||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
-1 |
F9 |
0 |
||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
F10 |
20 |
||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
+a |
0 |
0 |
-a |
0 |
F11 |
0 |
||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
+a |
0 |
1 |
+a |
0 |
F12 |
0 |
||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
F13 |
0 |
Use your Gaussian elimination program to solve this system of equations.
The Applet
Write an applet that draws the plane truss on the screen with text values annotating the loads and stresses as found by your Gaussian elimination program. The applet should also contain 4 locations for user entry of data. One location should be available for each of the load weights, and one location should be available for the maximum stress the truss members can take (all members have the same maximum stress). When the user changes any one of these values, the stresses should be recalculated and the truss should be redrawn with the new annotations. Members with zero stress should be drawn in blue. As stress on a member increases the color of the member should shift to yellow. If the stress on a member goes over the maximum stress value, then that member should be drawn in red.
See the example applet on the class web page. This example should serve as the basic functionality required for the project.