CSC 173, Fall 2001
Assignment 6: Logic
Solve the following problems:
-
(20 points)
Draw a truth table that shows all 16 Boolean functions of 2 variables, A
and B. Label the columns with their common names. You know most of
these:
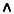 ,
,
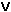 ,
,
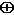 (exclusive or),
(exclusive or),
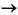 ,
,
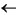 ,
,
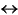 ,
NAND,
NOR,
true,
false,
A,
B,
,
NAND,
NOR,
true,
false,
A,
B,
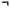 A,
A,
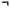 B.
What are the other two?
Which of the functions are commutative? Which are associative?
Which are complete? (You know that NAND and NOR are
complete; are any of the others?)
B.
What are the other two?
Which of the functions are commutative? Which are associative?
Which are complete? (You know that NAND and NOR are
complete; are any of the others?)
-
(Extra Credit: up to 10 points)
Suppose we had an algorithm to solve the tautology problem for
expressions in propositional logic. Show how this algorithm could be
used to
-
determine whether two expressions were equivalent.
-
solve the satisfiability problem (see the box on p. 673).
-
(15 points)
Prove the generalized DeMorgan's laws (equations 12.20(c) and 12.20(d)
in the book, p. 677) by
induction on k, using the basic laws (equations 12.20(a) and 12.20(b)).
-
(20 points)
Draw circuit diagrams for three different 4-bit adders (adders that take
two 4-bit inputs and compute a 4-bit output and a carry bit): a
ripple-carry adder, a carry-look-ahead (divide-and-conquer adder) and a
product-of-sums (conjunctive-normal-form) adder. For each of the
adders, give the total number of gates and the depth (the number of
gates on the longest path).
-
(Extra Credit: up to 15 points)
Determine, for each of the three classes of adders mentioned in the
previous questions, a general forumla for the total number of gates and
the depth, as a function of the number of bits N in each operand.
(This is not a big-O question: I'm looking for an exact answer.)
-
(10 points)
Translate the following statements into prenex CNF form (all quantifiers
on the outside, insides written as a logical product of sums):
-
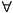 A[
A[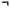 student(A)
student(A) 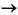 (
(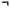 dorm_resident(A)
dorm_resident(A) 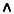
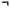
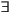 B[class(B)
B[class(B) 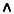 takes(A,B)])
takes(A,B)])
-
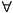 A
A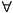 B [(
B [(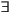 C[takes(A,C)
C[takes(A,C) 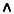 takes(B,C)])
takes(B,C)]) 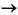 classmates(A,B)]
classmates(A,B)]
-
(10 points)
Suppose big(N) is interpreted to mean N > 2 and works(A,B,C,N) is
interpreted to mean AN + BN = CN.
State Fermat's last theorem
in predicate calculus, first in whatever form seems most intuitive, then
in prenex CNF. (Fermat's last theorem holds that the equation
AN + BN
= CN has no solutions over the non-zero integers for N > 2. It was
posed around 1630, but wasn't solved [by Andrew Wiles] until 1995.)
-
(15 points)
Prove the following by contradiction, using resolution. (Restate the
premises and the negation of the conclusion in CNF to create a database
[set] of terms, then apply resolution to obtain new terms, until you
derive the empty term [false].)
Premise one: (A
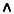 B)
B) 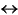 (C
(C 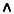 D).
Premise two:
(A
D).
Premise two:
(A 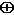 B).
Conclusion:
B).
Conclusion: 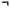 C
C 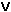
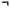 D.
D.
-
(10 points)
Prove that it is impossible to write a program that takes two arbitrary
programs as input and tells you whether they do the same thing (i.e.
whether given the same input they either both halt, with the same
output, or both run forever.) You may take as a given that the halting
problem is undecidable.
DUE DATE: noon, Friday December 14.
NO EXTENSIONS.
What/how to turn in
Bring hard-copy answers to Marty's Guenther's office (CBS 735).
There is no "trivia" assignment for this project.
Be sure to explain your answers.
In accordance with course policy,
you are permitted to discuss the
exercises with your peers, look things up in books, etc., but you
must actually write the answers yourself, in your own words, out of your
own head: no copying.
 Back to the grading page
Back to the grading page
 Back to the course home page
Back to the course home page
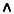 ,
,
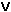 ,
,
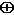 (exclusive or),
(exclusive or),
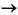 ,
,
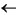 ,
,
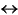 ,
NAND,
NOR,
true,
false,
A,
B,
,
NAND,
NOR,
true,
false,
A,
B,
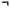 A,
A,
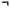 B.
What are the other two?
Which of the functions are commutative? Which are associative?
Which are complete? (You know that NAND and NOR are
complete; are any of the others?)
B.
What are the other two?
Which of the functions are commutative? Which are associative?
Which are complete? (You know that NAND and NOR are
complete; are any of the others?)
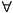 A[
A[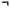 student(A)
student(A) 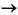 (
(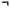 dorm_resident(A)
dorm_resident(A) 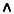
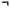
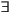 B[class(B)
B[class(B) 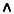 takes(A,B)])
takes(A,B)])
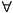 A
A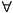 B [(
B [(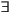 C[takes(A,C)
C[takes(A,C) 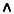 takes(B,C)])
takes(B,C)]) 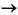 classmates(A,B)]
classmates(A,B)]
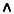 B)
B) 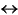 (C
(C 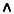 D).
Premise two:
(A
D).
Premise two:
(A 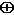 B).
Conclusion:
B).
Conclusion: 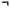 C
C 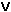
 D.
D.
 Back to the course home page
Back to the course home page