3-Way Teeter-Totter
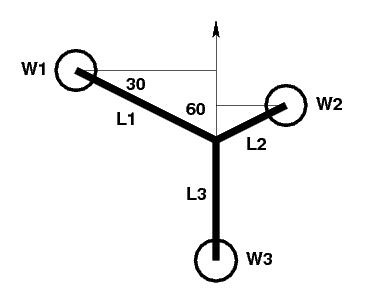
- 3 people, weights W1, W2, W3
- 3-armed teeter-totter, with arms 120° apart
- Total arm length = LT (a board we plan to cut up)
- Find arm lengths L1, L2, L3 so that system balances.
Equations
- Sum of lengths constraint:
L1 + L2 + L3 = LT
- First balance equation, using the fact that sin(30°) = 1/2):
W1 * L1 / 2 + W2 * L2 / 2 - W3 * L3 = 0
- Second balance equation:
W1 * L1 / 2 - W2 * L2 + W3 * L3 / 2 = 0
- Third balance equation:
W1 * L1 - W2 * L2 / 2 - W3 * L3 / 2 = 0
Note that we have 4 equations for 3 unknowns. The third balance equation is the sum of the first two, and hence it represents redundant information. This is known as a linear dependency
In matrix form we have:
[ 1 1 1 ] [L1] [LT] [ W1/2 W2/2 -W3 ] [L2] = [ 0] [ W1/2 -W2 W3/2] [L3] [ 0]
Also note that (most of) the same equations can be used to solve for different unknowns. For example, if we replace the sum-of-lengths constraint with a sum-of-weights, and start with known lengths, we have linear equations for the weights required to make the system balance.
- Sum of weights constraint:
W1 + W2 + W3 = WT
- First balance equation, written with the weights as the unknowns:
W1 * L1 / 2 + W2 * L2 / 2 - W3 * L3 = 0
- Second balance equation:
W1 * L1 / 2 - W2 * L2 + W3 * L3 / 2 = 0
In matrix form:
[ 1 1 1 ] [W1] [WT] [ L1/2 L2/2 -L3 ] [W2] = [ 0] [ L1/2 -L2 L3/2] [W3] [ 0]
